Предел и непрерывность тригонометрических функций
Непрерывность синуса и косинуса
Синус и косинус это отношения, которые определяется значением острого угла прямоугольного треугольника и сторонами треугольника.

Вот график синуса x и косинуса х
-Мы рассматриваем углы в радианах
-Вместо θ мы будем использовать x
f(x) = sin(x)



Очевидно, что так как h стремится к нулю, координаты P стремятся к соответсвующим координатам B.

Но по определению мы знаем, что
sin(0) = 0 и cos(0) = 1
Значения функций совпадают с теми пределами, когда x стремится к 0 (напоминает определение непрерывности, которое мы имеем).
limx → 0 sin(x) = sin(0) = 0 limx → 0 cos(x) = cos(0) = 1
Отсюда мы получаем следующую теорему
ОПРЕДЕЛЕНИЕ 2.7.1
Говорят, что функция f(x) является непрерывной в точке c если выполняются следующие условия
-f(c) определена
-limx → c f(x) существует
-limx → c f(x) = f(c)
Tеорема 2.8.1
Функции sin(x) и cos(x) - непрерывные
Proof
Пусть h = x - c. Отсюда x = h + c. Тогда x → c эквивалентно требованию h → 0
Функция f(x) непрерывна в c если следующие условия верны:
-f(c) определено
-limh → 0 f(h + c) существует
-limh → 0 f(h + c) = f(c)
Предположим, что
limx → 0 sin(x) = 0 и limx → 0 cos(x) = 1
Первые два условия непрерывности выполняются. Мы должны теперь показать что
limh → 0 sin(c + h) = sin(c)
Сейчас
limh → 0 sin(c + h) = limh → 0 [sin(c)cos(h) + cos(c)sin(h)] = limh → 0 sin(c)cos(h) + limh → 0 cos(c)sin(h) = sin(c)limh → 0 cos(h) + cos(c)limh → 0 sin(h) = sin(c)(1) + cos(c)(0) = sin(c)
Непрерывность других тригонометрических функций
tan(x) = sin(x)/cos(x)
tan(x) является непрерывной везде, кроме, где cos(x) = 0 что означает
x = ± φ/2, ± 3φ/2, ± 5φ/2, ... = ± kφ/2 (k = 1, 3, 5, ...)
Подобно, так как
cot(x) = cos(x)/sin(x)
sec(x) = 1/cos(x)
cosec(x) = 1/sin(x)
они все являются непрерывными на соответствующих интервалах, так как непрерывны sin(x) и cos(x).
Получение пределов сжатием
Мы будем использовать теорему сжатия (теорему о двух милиционерах) для нахождения пределов
limx → 0 sin(x)/x = 1
limx → 0 [1 - cos(x)]/x = 0 Рассмотрим график


Вот проблема:
- Когда x стремится к нулю, и верх, и низ функции стремится к нулю.
- sin(x) стремится к нулю и это означает, что дробь в целом стремится к нулю.
- x стремится к нулю означает, что функция в целом стремится к +∞.
Но мы не можем записать эти функции в иной форме, используя алгебраические методы, чтобы решить эту проблему. Мы воспользуемся другим методом. Один из таких методов получен с помощью следующей теоремы:
Теорема сжатия (Теорема о двух милиционерах)
Пусть f, g и h будет функцией удовлетворяющей g(x)≤f(x)≤h(x) для всех x в некоторых открытых интервалах, содержащих точку a, с возможными исключениями, что это не выполняется в точке.
Если g и h имеют те же самые пределы когда x стремится к a, говорят, что
limx → a g(x) = limx → a h(x) = L
тогда f также имеет такой же предел, когда x стремится к a, то есть s
limx → a f(x) = L
Example:
Используйте теорему сжатия, чтобы найти
limx → 0 x2sin2(1/x)
Решение
Так как 0 ≤ sin(x) ≤ 1, тогда 0 ≤ sin2(x) ≤ 1 и также 0 ≤ sin2(1/x) ≤ 1
Умножим последнее неравенство на x2
0 ≤ x2sin2(1/x) ≤ x2
Но limx → 0 0 = limx → 0 x2 = 0
Тогда, согласно теореме сжатия
limx → 0 x2sin2(1/x) = 0
Перед доказательством следующей теоремы, посмотрим на следующую формулу.
В доказательстве будут использованы основные факты об окружностях и площадях секторов с углом θ радианами и радиусом r
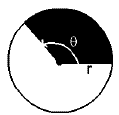
Площадь данного сектора определяется как
A = (1/2).r2θ
Tеорема 2.8.3
limx → 0 sin(x)/x = 1
Пусть x будет такое, что 0 < x < φ/2 or -φ/2 < x < 0
Мы сделали предположение, что
0 < x < φ/2
Также работает когда -φ/2 < x < 0

Из рисунка
0 < area of ΔOBP = (1/2) base.height = (1/2) (1).sin(x) = (1/2) sin(x)
area of sector OBP = (1/2)(1)2.x = (1/2)x
area of ΔOBQ = (1/2) base.height = (1/2) (1).tan(x) = (1/2)tan(x)
Так, вышеприведенное неравенство превращается в
0 < (1/2)sin(x) < (1/2)x < (1/2)tan(x)
Умножая это на 2/sin(x)
1 < x/sin(x) < 1/cos(x)
После соответсвующего преобразования получим
cos(x) < sin(x)/x < 1
Использование теоремы сжатия приводит к
limx → 0 cos(x) < limx → 0 sin(x)/x < limx → 0 1 = 1 < limx → 0 sin(x)/x < 1
Так как средний член между 1 и 1, тогда это должно быть равно 1

 Меню
Меню