Сфера (шар)

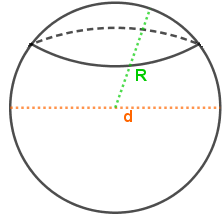
Шаровая поверхность или сфера - это поверхность, образованная совокупностью точек равноудалённых от некоторой точки, называемой центром.

Радиус это расстояние от центра до поверхности.

Диаметр сферы - это хорда, проведённая через центр и соединяющая две точки на поверхности шара.

Площадь поверхности:
Площадь поверхности $=4\pi R^2 = \pi d^2=\sqrt[3]{36\pi V^2}$

Объём:
Объём $ =\frac43 \pi R^3 = \frac{\pi}{6}d^3 = \frac{1}{6}\sqrt{\frac{s^3}{\pi}}$

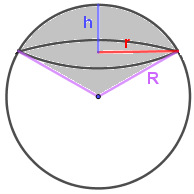
Шаровой сектор это часть шара ограниченная коничекой поверхностью с вершиной в центре шара.

Площадь изогнутой поверхности шарового сектора (исключая поверхность конуса):
$S = 2 \pi Rh$

Полная площадь поверхности (включая поверхность конуса):
$S=\pi R(2h + r)$

Объём:
Объём $= \frac{2\pi R^2h}{3}$

Шаровой сегмент - это часть шара, отсекаемая от него какой-либо плоскостью.

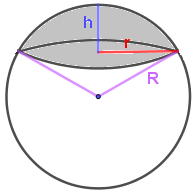
Площадь изогнутой поверхности шарового сегмента:
Площадь изогнутой поверхности $=2\pi Rh = \pi d h=\pi(r^2+h^2)$

Общая площадь поверхности $=2\pi R h + \pi r^2 = \pi(h^2 + 2r^2) = \pi h(4R - h)$

Объём:
Объём $\frac{\pi h^2}{3}(3R - h) = \frac{\pi h}{6}(3r^2 + h^2)$

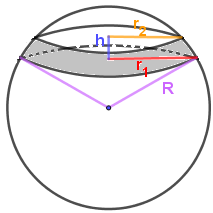
Шаровой слой - это часть шара, заключённая между двумя параллельными секущими плоскостями.

Площадь изогнутой поверхности (исключая площадь сечений):
Площадь изогнутой поверхности $=2\pi R h$

Площадь поверхности (включая площадь сечений):
Площадь поверхности $=2\pi Rh + \pi r_1^2 + \pi r_2^2 = \pi(2Rh + r_1^2 + r_2^2)$

Объём:
Объём $ = \frac{1}{6}\pi h(3r_1^2+3r_2^2+h^2)$