Окружность

Окружность - геометрическое место точек плоскости, расстояние от которых до центра окружности равно.

Центр окръжности

Радиус: расстояние от центра окружности до его границы.

Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.

$d = 2\cdot r$

Периметр (длина окружности): длина границы окружности.

Длина окружности $= \pi \cdot$ диаметр $= 2 \cdot \pi \cdot$ радиус
Длина окружности $= \pi \cdot d = 2 \cdot \pi \cdot r$

$\pi$ - pi: число, равное 3,141592... или $\approx \frac{22}{7}$, то есть отношение $\frac{\text{длины окружности}}{\text{диаметр}}$ любого окружности.

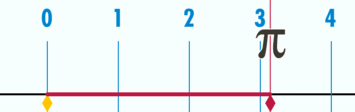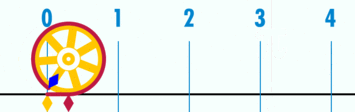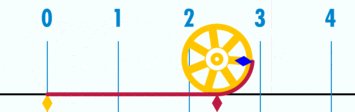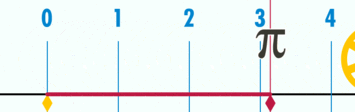
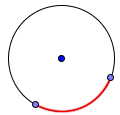
Дуга: изогнутая линия, которая является частью окружности.

Дуги окружности измеряется в градусах или радианах.
Например: 90° или $\frac{\pi}{2}$ - четверть круга,
180° или $\pi$ - половина круга.
Сумма всех дуг окружности составляет 360° или $2\pi$

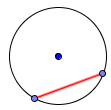
Хорда: отрезок прямой, соединяющей две точки на окружности.

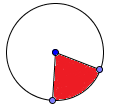
Сектор: похож на часть пирога (клин).

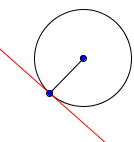
Касательная к окружности: прямая, перпендикулярна к радиусу, и имеющая ТОЛЬКО одну общую точку с окуржностью.

Формулы

Длина окружности $=\pi \cdot \text{диаметр} = 2\cdot \pi \cdot \text{радиус}$

Площадь круга $= \pi \cdot$ радиус²

Радиус обозначается как r, диаметр как d, длина окружности как P и площадь как S.

Площадь сектора круга

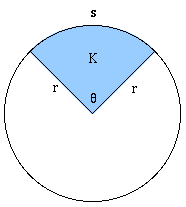
Площадь сектора круга K: (с центральным углом $\theta$ и радиусом $r$).
Если угол $\theta$ в градусах, тогда площадь = $\frac{\theta}{360} \pi r^2$
Если угол $\theta$ в радианах, тогда площадь, тогда площадь = $\frac{\theta}{2} r^2$

Углы

Центральный угол

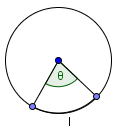
Если длина дуги составляет $\theta$ градуов или радиан, то значение центрального угла также $\theta$ (градусов или радиан).

Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах ...) вы можете найти значение её соответствующего центрального угла ($\theta$) по формуле:

$l$ - длина дуги.

Вписанный угол

Вписанный угол это угол с вершиной на окружности и со сторонами, которые содержат хорды окружности.
На рисунке, угол APB это вписанный угол.

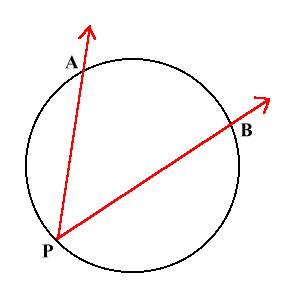
Величина вписанного угла равна половине дуги, на которую он опирается.

Пример:
$\widehat{AB} = 84^\circ$
$\angle APB = \frac{84}{2} = 42^\circ$

Углы между двумя хордами

Случай 1: два секущие пересекаются внутри окружности.

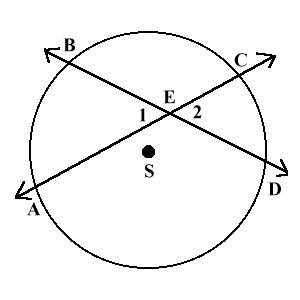
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны $\frac{1}{2}(60^\circ + 50^\circ)=55^\circ$

Случай 2: две секущие пересекаются вне окружности.

Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.

$\angle ABC =\frac{1}{2}(x - y)$

На рисунке дуга AB=80° и дуги CD=30°.
$\angle ABC = \frac{1}{2}(80 - 30) = \frac{1}{2} \cdot 50 = 25^\circ$

Хорды

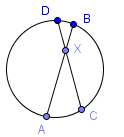
Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда: