Формулы площади
Стандартное обозначение площади - S
Площадь
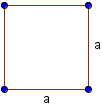
Пусть длина стороны квадрата равна a, тогда формул квадрата:
Прямоугльник

Пусть длины сторон прямоугольника равны a и b
Параллелограмм
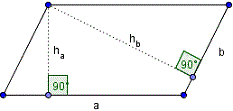
Пусть длины сторон параллелограмма равны a и b и
ha это высота на сторону a,
и hb это высота на сторону b
Формула площади параллелограмма:
Трапеция

Допустим, что длины параллельных сторон трапеции имеют длину a и b и расстояние между двумя основами h (высота трапеции). Тогда формула площади:
Площадь круга
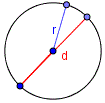
$S = \pi\cdot r^2$
$\pi=3,14$
Площадь прямоугольного треугольника
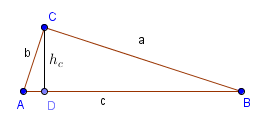
$S=\frac{a \cdot b}{2}$
$S=\frac{c \cdot h_c}{2}$
Треугольник
ABC - треугольник

длина его сторон: a, b, c и длина его высот: ha, hb и hc.
Площадь треугольника по трем сторонам
$S = \sqrt{p(p - a)(p - b)(p - c)}$, где $p = \frac{a + b + c}{2}$
Это известна как формула Герона, и $p$ называется полупериметром.
Если исключим полупериметр ($p$), формула будет выглядеть так:
$S=\frac14\sqrt{4a^2b^2-(a^2+b^2-c^2)^2}$
Площадь треугольника - калькулятор
Стороны треугольника:Другие формулы площади треугольника
$S = \frac{a\cdot b\cdot \sin C}{2} = \frac{a\cdot c\cdot \sin B}{2} = \frac{b\cdot c\cdot \sin A}{2}$
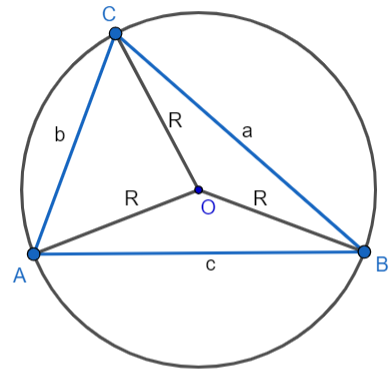
$S = R^2\sin(A) \cdot \sin(B) \cdot \sin(C) = \frac{abc}{4R}$
где R - радиус описанной окружности
Площадь параллелограмма(ромба)
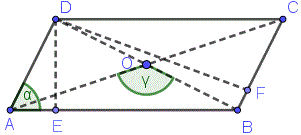
$S = AB\cdot DE = BC \cdot DF$
$S = AB \cdot AD \sin \alpha$
$S = \frac12 AC \cdot BD \sin \gamma$
Площадь выпуклого четырехугольника

$S = \frac12 AC \cdot BD \sin \varphi $
Площадь правильного многоугольника

$S = \frac14 n\cdot a^2\cdot \text{ctg}(\frac{\pi}{n})$
n - число ребер(вершин).
$\pi=3,14159265359$

 Меню
Меню