Формулы объема

Стандартное обозначение объема есть V. Этим мы измеряем количество (наример, воды), которая может заполнить фигуру.
Только пространственные фигуры имеют объем. Например, треугольники, квадраты не имеют объема, но шар имеет объем (потому что он может быть заполнен чем-то, например водой).

Прямоугольный параллелепипед

Прямоугольный параллелепипед это фигура, все стороны которой - прямоугольники.
Если длины стороны прямоугольника в основе есть a и b и третье ребро c
тогда формула объема есть:

$V = a \cdot b \cdot c$

Площадь поверхности:

S = $2(a \cdot b + a \cdot c + b \cdot c)$

Куб

Куб есть параллелепипедом, все ребра (стороны) которого равны.

Если длина стороны куба равна a, тогда формула объема:

$V = a.a.a = a^3$

Площадь поверхности:

$S = 6a \cdot a = 6a^2$

Параллелепипед

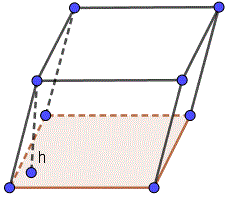
Параллелепипед это фигура, все стороны которой - параллелограммы. Если площадь основы равна S и высота параллелепипеда равны h,
то формула объема есть:

$V = S \cdot h$

Пирамида

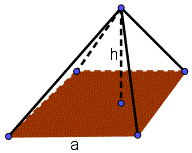
Пирамида это фигура, основа которой есть треугольник, параллелограмм (квадрат, прямоугольник) или другая фигура с n-углами и треугольными сторонами.
Если площадь основы есть S и высота пирамиды есть h,
тогда формула ее объема есть:

$V = \frac{1}{3} \cdot S \cdot h$

Правильный тетраэдр

$V = \frac{\sqrt{2}\cdot a^3}{12}$

Площадь поверхности:

$S = \sqrt{3}\cdot a^2$

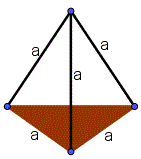
Прямой круговой конус

Конус это фигура с основанием в виде окружности и имеющая одну вершину, как у пирамиды.
Если площадь основы есть S и длиныа стороны конуса равна h,
то формула объема есть:

$V = \frac{1}{3} \cdot S \cdot h = \frac{1}{3} \cdot \pi \cdot r^2\cdot h$

Формула площади боковой поверхности конуса:

$S=\pi\cdot r \cdot l$

Формула площади полной поверхности конуса (то есть сумма площадей боковой поверхности и основания):

$S=\pi\cdot r(r + l)$

Сфера

Сфера есть шар.
Она имеет радиус - расстояние от центральной точки сферы к поверхности. Если длина радиуса есть R, то формула объема есть:

$V = \frac{4}{3} \cdot \pi \cdot r^3$

Площадь поверхности:

$S = 4\cdot\pi\cdot r^2$

Цилиндр

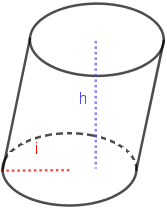
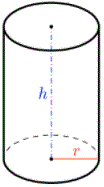
Цилиндр это фигура с двумя параллельными окружностями.
Если ралиус основы равен r и высота (расстояние между основами) цилиндра есть h,
то его объем вычисляется по формуле:

$V = \pi \cdot r^2 \cdot h$

Прямой круговой цилиндр

Объём

$V = \pi \cdot r^2 \cdot h$

Площадь боковой поверхности:

$S = 2\cdot\pi\cdot r \cdot h$

Площадь полной поверхности:

$S = 2\cdot\pi\cdot r(h + r)$

Тест: объём и площадь поверхности