Эллипс, парабола, гипербола

Эллипс с центром в $C(x_0 \textrm{ , } y_0)$ и большей осью, параллельной $x$ ось

Длина большей оси $A'A = 2a$
Длина малой оси $B'B = 2b$
Расстояние от центра $C$ к фокусу $F$ или $F'$ есть
$c = \sqrt{a^2 - b^2}$
Эксцентриситет = $\epsilon = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a}$
Уравнение в прямоугольных координатах:
$\frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1$
Уравнение в прямоугольных координатах если $C$ есть в $O$:
$r^2 = \frac{a^2b^2}{a^2 \textrm{ sin }^2 \theta + b^2 \textrm{ cos }^2 \theta}$
Уравнение в прямоугольных координатах если $C$ на $x$ оси и $F'$ в $O$:
$r = \frac{a(1 - c^2)}{1 - c \textrm{ cos } \theta}$
Если $P$ есть любая точка на эллипсе, $PF + PF' = 2a$
Если большая ось параллельна $y$ оси, меняем местами $x$ и $y$ вверху или заменяем $\theta$ на $\frac{1}{2}\pi - \theta$ [или $90^\circ - \theta$]

Парабола с осью, параллельной $x$ ось

Если вершина в $A(x_0 \textrm{ , } y_0)$ и расстояние между $A$ к фокусу$f$ есть $a > 0$, уравнение параболы есть следующее, если парабола открыта справа

$(y - y_0)^2 = 4a(x - x_0)$

Если парабола открыта слева
$(y - y_0)^2 = -4a(x - x_0)$

Если фокус находится в центре координат, уравнение в полярных координатах есть
$r = \frac{2a}{1 - \textrm{ cos } \theta}$



В случае, если ось параллельна $y$ оси, меняя $x$ и $y$ или заменяя $\theta$ на $\frac{1}{2}\pi - \theta$ [или $90^\circ - \theta$].

Гипербола с центром $C(x_0 \textrm{ , } y_0)$ и большей осью, параллельной к $x$ ось

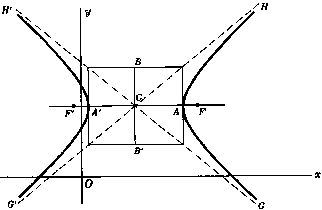
Длина большой оси $A'A = 2a$
Длина малой оси$B'B = 2b$
Расстояние от центра $C$ к фокусу $F$ или $F'$ есть
$c = \sqrt{a^2 + b^2}$
Эксцентриситет = $\epsilon = \frac{c}{a} = \frac{\sqrt{a^2 + b^2}}{a}$
Уравнение в прямоугольных координатах:
$\frac{(x - x_0)^2}{a^2} - \frac{(y - y_0)^2}{b^2} = 1$
Наклоны асимптоты $G'H$ и $GH' = \pm \frac{b}{a}$
Уравнение в полярных координатах, если $C$ в $O$:
$r^2 = \frac{a^2b^2}{b^2 \textrm{ cos }^2 \theta - a^2 \textrm{ sin }^2 \theta}$
Уравнение в полярных координатах, если $C$ на $X$ оси и $F'$ в $O$:
$r = \frac{a(c^2 - 1)}{1 - \epsilon \textrm{ cos } \theta}$
Если $P$ в любой точке на гиперболе, $PF - PF' = \pm 2a$ [в зависимости от ветки]
Если большая ось параллельна $y$ оси, меняя $x$ и $y$ вверху или заменяя $\theta$ на $\frac{1}{2}\pi - \theta$ [или $90^\circ - \theta$].

Гипербола - анимация