Visina trougla

Udaljenost između vrha i naspramne stranice se naziva visina trougla. Zapravo, najkraća udaljenost između vrha trougla i suprotne stranice.

Napomena: Svaki trougao ima tri visine koje se seku u jednoj tački koju nazivamo ortocentar.

Visine oštrouglog trougla

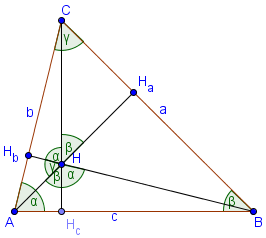
Ortocentar je unutrašnja tačka trougla.

∠ AHB = 180 - γ = α + β
∠ BHC = 180 - α = β + γ
∠ AHC = 180 - β = α + γ
∠ AHH_c = β, ∠ BHH_c = α, ∠ BHH_a = γ

Visine tupouglog trougla

Ortocentar leći izvan trougla.
Takođe, dve visine uvek leće izvan trougla.
∠ AHH_c = ∠ CBA = β
∠ H_cHB = ∠ CAB = α

Pravougli trougao

Visina AH_a se podudara sa AC.
Visina BH_b se podudara sa BC.
Ortocentar H se podudara sa C.
∠ ACH_c = β, ∠ BCH_c =α

Formule

$AH_a:BH_b:CH_c=\frac{1}{a}:\frac{1}{b}:\frac{1}{c}$

$\frac{a}{AH_a}=\frac{b}{BH_b}=\frac{c}{\frac{AH_aBH_b}{CH_c}}$

R - poluprecnik opisanog kruga
r - poluprecnik upisanog kruga
p - je polovina obima: (a + b + c)/2

$AH_a=b \sin\gamma=c \sin\beta=\frac{a \sin\beta \sin\gamma}{\sin\alpha}=$

$=2R \sin\beta\ \sin\gamma=\frac{bc}{2R}=\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{a}$

$BH_b=a\ \sin\gamma=c\ \sin\alpha=\frac{b\ \sin\alpha\ \sin\gamma}{\sin\beta}=$
$=2R\ \sin\alpha \sin \gamma=\frac{ac}{2R}=\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{b}$

$CH_c=a\ \sin\beta=b\ \sin\alpha=\frac{c\ \sin\alpha\ \sin\beta}{\sin\gamma}=$
$=2R\ \sin\alpha \sin \beta=\frac{ab}{2R}=\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{c}$

$\frac{1}{AH_a}+\frac{1}{BH_b}+\frac{1}{CH_c}=\frac{1}{r}$