Kružnica i krug

Kružnica je kriva linija, koju čine sve tačake u ravni podjednako udaljene od date tačke – centra.

Krug je figura, koju čine sve tačke ravni čije rastojanje od date tačke - centra nije veće od određene vrednosti - poluprečnika kruga.
Krug

Centar : Centar kružnice

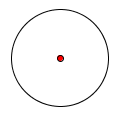
Poluprečnik : udaljenost od centra kružnice do bilo koje njene tačke.
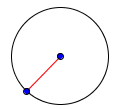
Poluprečnik kružnice

Prečnik : Najveća udaljenost od jedne tačke kruga do druge. Prečnik = 2 x poluprečnik .

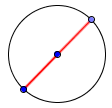
Obim : Ukupna dužina kružnice. Jednaka je $\pi \times$ prečnik.
Obim

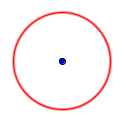
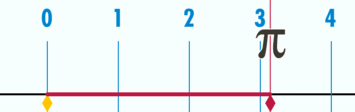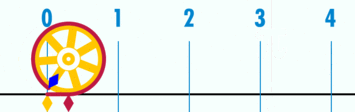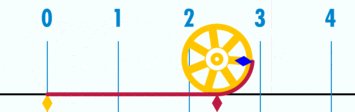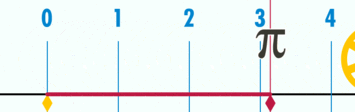
$\pi$ - pi: broj jednak 3.141592... ili $\approx \frac{22}{7}$, što je $\frac{\text{obim}}{\text{prečnik}}$ bilo kog kruga.

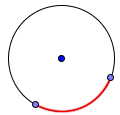
Kružni luk: kriva linija koja je deo kružnice.

Kružni luk se meri stepnima ili radijanima – na primer 90° ili $\frac{\pi}{2}$ - četvrtina kružnice, 180° ili $\pi$ - polovina kružnice. Luk je manji od 360° (ili $2\pi$) jer je to cela kružnica.

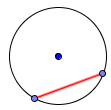
Tetiva : duž unutar kružnice koja dodiruje 2 njene tačke.
Tetiva

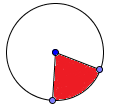
Kružni isečak : izgleda kao parče pite (kružni klin).

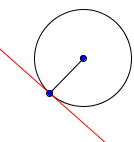
Tangenta : linija normalna na prečnik kružnice koja dodiruje SAMO jednu tačku kružnice.
Tangenta kružnice

Formule

Formula za pronalaženje obima kruga je $\pi\ \cdot $ prečnik $= 2 \cdot \pi \cdot$ poluprečnik

Formula za pronalaženje površine kruga je $\pi\ \cdot$ poluprečnik $\cdot$ poluprečnik

Standardna oznaka za poluprečnik je r,
za prečnik - R,
za obim - O,
a za površinu P.

Formule:

$O = \pi \cdot R = 2 \cdot \pi \cdot r$
$P = \pi \cdot r^2$

Površina kružnog isečka

$r$ je poluprečnik kruga.
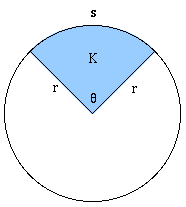
$\theta$ je veličina centralnog ugla.
Ako je ugao θ izražen u stepenima, onda je površina = $\frac{\theta}{360} \pi r^2$ Ako je ugao θ izražen u radijanima, onda je površina = $\frac{\theta}{2} r^2$

Uglovi

Centralni ugao

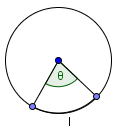
Ako je dužina luka $\theta$ stepeni ili radijana onda je veličina centralnog ugla takođe $\theta$(stepeni ili radijana).

Ako znamo dužinu luka (u inčima, jardama, stopama, centimetrima, metrima…) možemo pronaći veličinu odgovarajućeg centralnog ugla ($\theta$) formulom:

$\theta = 360 \cdot \frac{l}{O} = \frac{360 \cdot l}{2 \cdot \pi \cdot r} = \frac{180 \cdot l}{\pi \cdot r}$

$l$ je dužina luka.

Periferijski ugao

Periferijski ugao je sačinjen od dve tetive i temena koje se nalazi na kružnici.
$\angle APB$ je periferijski ugao

Veličina periferijskog ugla je jednaka polovini veličine njegovog luka na kružnici.

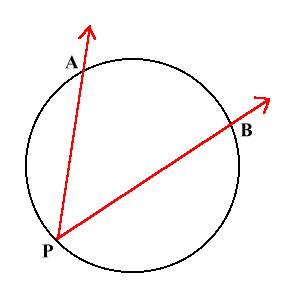
Primer:
Luk $\widehat{AB}$ iznosi 84°. Veličina $\angle APB = \frac{84}{2} = 42^\circ$

Uglovi izmedju dve sečice

1. Slučaj: dve sečice koje se seku unutar kruga.

Kada se dve sečice seku unutar kruga, veličina svakog od formiranih uglova jednaka je polovini zbira lukova.
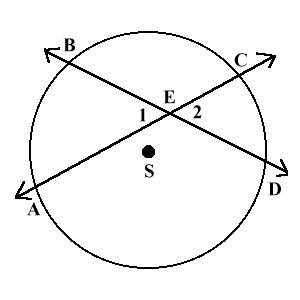
Na slici luk AB je iznosi 60° a luk CD iznosi 50°.
Dakle veličine uglova 1 i 2 iznose ½(60° + 50°) = 55°

2. Slučaj: dve sečice se seku izvan kruga.
sečice se seku izvan kruga

Veličina formiranog ugla je jednaka polovini razlike lukova.

$\angle ABC =\frac{1}{2}(x - y)$

Na primer: Ako je veći luk 80° a manji 30° onda je $\angle ABC = \frac{1}{2}(80 - 30) = \frac{1}{2} \cdot 50 = 25^\circ$

Formula za tetive koje se seku

dve tetive koje se seku
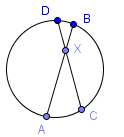
Kada se dve tetive seku unutar kruga onda:

$AX \cdot XB = CX \cdot XD$