Srednja linija trapeza i trougla

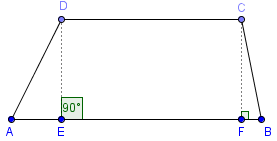
Stranice trapeza koje su paralelne se nazivaju osnovice dok se stranice koje nisu paralelne nazivaju kraci. Ako su kraci jednake dužine, onda je trapez jednakokraki.
DE i CF se nazivaju visine trapeza.

AD i BC su kraci trapeza.
AB i CD su paralelne stranice.

Srednja linija trapeza

Duž koja spaja sredine dve neparalelne stranice trapeza se naziva srednja linija.
MN je srednja linija ABCD trapeza. M je sredina stranice AB, dok je N sredina stranice BC.

MN srednja linija, AB i CD su osnovice, AD i BC su kraci.

Srednja linija trapeza je paralelna sa osnovicama. U našem slučaju - MN || AB || DC.

Teorema 1:

Teorema 2:

ili
$MN = \frac{AB + DC}{2}$

Srednja linija trougla

Duž koja je određena sredinama dveju stranica trougla se naziva srednja linija trougla. Ona je paralelna sa trećom stranicom i jednaka je polovini njene dužine.
Teorema: Ako duž seče sredinu jedne stranice trougla i paralelna je sa drugom stranicom istog trougla, tada ta duž polovi treću stranicu.

AM = MC i BN = NC =>

Primena svojstava srednjih linija trapeza i trougla

Podela duži na jednake delove.

Zadatak: Podeli datu duž AB na 5 jednakih delova.
Rešenje:
Neka je p proizvoljna prava koja prolazi kroz tačku A i p ne leži na AB. Nacrtaćemo pet jednakih delova na p.
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅
Povezaćemo A₅ sa B i nacrtati prave kroz tačke A₄, A₃, A₂ i A₁ koje su paralelne sa A₅B. One seku AB respektivno u tačkama B₄, B₃, B₂ i B₁. Ove tačke dele duž AB na pet jednakih delova. Zaista, iz trapeza BB₃A₃A₅ vidimo da je BB₄ = B₄B₃. Na isti način, iz trapeza B₄B₂A₂A₄, dobijamo da je B₄B₃ = B₃B₂

Dok je iz trapeza B₃B₁A₁A₃, B₃B₂ = B₂B₁.
Tada iz B₂AA₂, sledi da je B₂B₁ = B₁A. Konačno dobijamo:
AB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B
Jasno je da ako je AB potrebno podeliti na neki drugi broj jednakih delova, treba da projektujemo isti broj jednakih delova na p i nastavljamo na gore opisan način.