Curvas planas especiales

Lemniscata
Ecuación en coordenadas polares:
$r^2=a^2\cos2\theta$

Ecuación en coordenadas rectangulares:
$(x^2+y^2)^2=a^2(x^2-y^2)$

Ángulo entre $AB'$ o $A'B$ y el eje $x$ $= 45^\circ$

Área de un bucle $=\frac{a^2}{2}$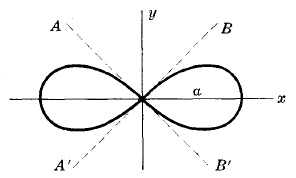

Cicloide
Ecuaciones en forma paramétrica:
$\left\{\begin{array}{lr}x=a(\phi-\text{sen}\phi)\\ y=a(1-\cos\phi)\end{array}\right.$

Área de un arco$=3\pi a^2$

Longitud de arco de un arco $=8a$

Esta es una curva descrita por un punto $P$ sobre un círculo de radio $a$ rodando a lo largo del eje $x$.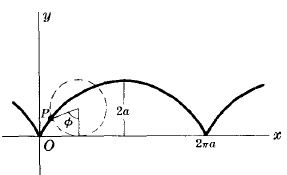

Hipocicloide con cuatro cúspides
Ecuación en coordenadas rectangulares:
$x^\frac{2}{3}+y^\frac{2}{3}=a^\frac{2}{3}$

Ecuaciones en forma paramétrica:
$\left\{\begin{array}{lr}x=a\cos^3\theta\\ y=a\sen^3\theta\end{array}\right.$

Área delimitada por curva $=\frac{3\pi a^2}{8}$

Longitud de arco de toda la curva $=6a$

Esta es una curva descrita por un punto $P$ en un circulo de radio $\frac{a}{4}$ a medida que rueda en el interior de un círculo de radio $a$.

Cardioide
Ecuación: $r=a(1+\cos\theta)$

Área delimitada por la curva $=\frac{3\pi a^2}{2}$

Longitud de arco de la curva $=8a$

Esta es la curva descrita por un punto $P$ de un círculo de radio $a$ a medida que rueda en el exterior de un círculo fijo de radio $a$.La curva es también un caso especial del caracol (limacón) de Pascal.

Catenaria
Ecuación:
$y=\frac{a(e^\frac{x}{a}+ e^{-\frac{x}{a}})}{2}=a\cosh\frac{x}{a}$

Esta es una curva en la que una cadena pesada y uniforme se cuelga si se suspende verticalmente desde puntos fijos $A$ y $B$.

Rosa de tres pétalos
Ecuación: $r=a\cos3\theta$

La ecuación $r=a\cos3\theta$ Es una curva similar obtenida girando la curva en sentido contrario a las agujas del reloj $30^o$ o $\frac{\pi}{6}$ radianes.

En general $r=a\cos n\theta$ or $r=a\sen n\theta$ tiene $n$ pétalos si $n$ es impar.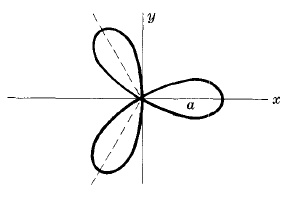

Rosa de cuatro pétalos
Ecuación: $r=a\cos2\theta$

La ecuación $r=a\sen2\theta$ es una curva similar obtenida girando la curva en sentido contrario a las agujas del reloj $45^o$ o $\frac{\pi}{4}$ radianes.

En general $r=a\cos n\theta$ o $r=a\sen n\theta$ tiene $2n$ pétalos si $n$ es par.

Epicicloide
Ecuaciones paramétricas
$\left\{\begin{array}{lr}x=(a+b)\cos\theta-b\cos\left(\frac{a+b}{b}\right)\theta\\ y=(a+b)\sen\theta-b\sen\left(\frac{a+b}{b}\right)\theta\end{array}\right.$

Esta es una curva descrita por un punto $P$ en un circulo de un radio $b$ a medida que rueda en el exterior de un círculo de radio $a$. El cardioide es un caso especial de un epicicloide.

Hipocicloide general
Ecuaciones paramétricas:
$\left\{\begin{array}{lr}x=(a-b)\cos\phi+b\cos\left(\frac{a-b}{b}\right)\phi\\ y=(a-b)\sen\phi-b\sen\left(\frac{a-b}{b}\right)\phi\end{array}\right.$

Esta es una curva descrita por un punto $P$ en un circulo de radio $b$ a medida que rueda en el exterior de un círculo de radio $a$.

Si $b = \frac{a}{4}$, la curva es un hipocicloide con cuatro cúspides.

Trocoide
Ecuaciones paramétricas:
$\left\{\begin{array}{lr}x=a\phi-b\sen\phi\\ y=a-b\cos\phi\end{array}\right.$

Esta es una curva descrita por un punto $P$ a una distancia $b$ del centro de un círculo de radio $a$ mientras el círculo rueda sobre el eje $x$.
Si $b < a$, la curva es como se muestra en Fig.11-10 y se llama cicloide acortada.
Si $b > a$, the curve is as shown on Fig.11-11 and is called cicloide alargada.
Si $b = a$, la curva es un cicloide.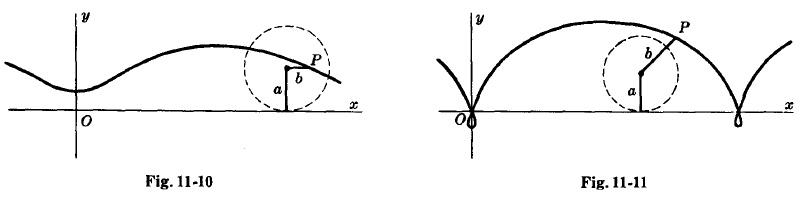

Tractriz
Ecuaciones paramétricas:
$\left\{\begin{array}{lr}x=a(\ln\cot\frac{1}{2}\phi-\cos\phi)\\ y=a\sen\phi\end{array}\right.$

Esta es una curva descrita por el punto final $P$ de una cuerda tensa $PQ$ de longitud $a$ mientras el otro extremo $Q$ es movido a lo largo del eje $x$.

La curva de Agnesi (llamada impropiamente la bruja de Agnesi)
Ecuación en coordenadas rectangulares: $y=\frac{8a^3}{x^2+4a^2}$

Ecuaciones paramétricas:
$\left\{\begin{array}{lr}x=2a\cot\theta\\ y=a(1-\cos2\theta)\end{array}\right.$

En la figura la recta variable $OA$ intersecta $y = 2a$ y el círculo de radio $a$ con centro $(0,a)$ en $A$ y $B$ respectivamente. Cualquier punto $P$ sobre la "bruja" (la curva) se ubica mediante la construcción de líneas paralelas a los ejes $x$ e $y$ a través de $B$ y $A$ respectivamente y determinando el punto $P$ de intersección.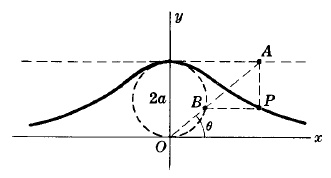

Folium de Descartes
Ecuación en coordenadas rectangulares:
$x^3+y^3=3axy$

Ecuaciones paramétricas:
$\left\{\begin{array}{lr}x=\frac{3at}{1+t^3}\\ y=\frac{3at^2}{1+t^3}\end{array}\right.$

Área del bucle $\frac{3a^2}{2}$

Ecuación de la asíntota: $x + y + a = 0$.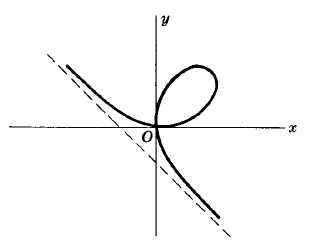

Envolvente (Involuto) de un círculo
Ecuaciones paramétricas:
$\left\{\begin{array}{lr}x=a(\cos\phi+\phi\sen\phi)\\ y=a(\sen\phi-\phi\cos\phi)\end{array}\right.$

Esta es una curva descrita por el punto final $P$ de una cuerda mientras se desenrolla de un círculo de radio $a$ mientras se mantiene tensa.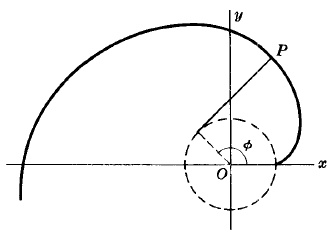

Evoluta de una elipse
Ecuación en coordenadas rectangulares:
$(ax)^\frac{2}{3}+(by)^\frac{2}{3}=(a^2-b^2)^\frac{2}{3}$

Ecuaciones paramétricas:
$\left\{\begin{array}{lr}ax=(a^2-b^2)\cos^3\theta\\ by=(a^2-b^2)\sen^3\theta\end{array}\right.$
Esta curva es la envolvente de las normales a la elipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.

Óvalo de Cassini
Ecuación polar: $r^4+a^4-2a^2r^2\cos2\theta=b^4$.

Esta es la curva descrita por el punto $P$ de tal manera que el producto de sus distancias desde dos puntos fijos [separados una distancia $2a$] es una constante $b^2$.

La curva es como en las figuras según $b < a$ o $b > a$ respectivamente.

Si $b = a$, la curva es una lemniscata

Caracol (Limacón) de Pascal
Ecuación polar: $r = b + a\cos\theta$

Sea $OQ$ una línea que une el origen $O$ con cualquier punto $Q$ de un círculo de diámetro $a$ que pasa a través de $O$. Entonces la curva es el lugar geométrico de todos los puntos $P$ tales que $PQ = b$.

La curva es como en lass siguiente figuras según si $b > a$ o $b < a$ respectivamente. Si $b = a$, la curva es un cardioide.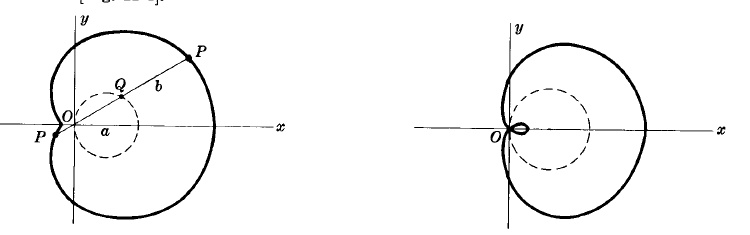

Cisoide de Diocles
Ecuación en coordenadas rectangulares: $y^2=\frac{x^3}{2a - x}$

Ecuaciones paramétricas:
$\left\{\begin{array}{lr}x=2a\sen^2\theta\\ y=\frac{2a\sen^3\theta}{\cos\theta}\end{array}\right.$

Esta es la curva descrita por un punto $P$ tal que la distancia $OP =$ distancia $RS$. Se usa en problemas de duplicación de un cubo, p.ej.: encontrar el lado de un cubo que tiene el doble del volumen de un cubo dado.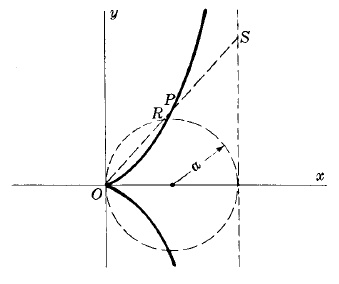

Espiral de Arquímedes
Ecuación polar: $r = a\theta$