Valores absolutos

En esta clase discutiremos:

Valores absolutos
Desigualdades que involucran valores absolutos.
El teorema (√a²=|a|)
El teorema de la desigualdad

Definición

El valor absoluto o magnitud de un número real a se denota por |a| y se define como
$|a| = \begin{cases} a \ \ \text{ si } a \ge 0 \\ -a\ \ \text{ si } a < 0\end{cases}$

Ejemplo
|5|=5 Dado que 5>0
|-4/7|= -(-4/7) = 4/7 Dado que -4/7<0
|0|=0 Dado que 0≥0

Observación
|a| es un número no negativo para todos los valores de a y
-|a|≤ a ≤ |a|
Si a de por sí es negativa, entonces -a es positiva y + a es negativa !!!

Ejemplo
Resuelva |x-3|=4
Solución

x-3= 4

x= 7

-(x-3)= 4
x-3= -4
x= -1

Ejemplo
Resuelva |3x-2|=|5x+4|

3x-2 = 5x+4
3x-5x = 4+2
-2x = 6
x = -3

3x-2 = -(5x+4)
.
.
x = -1/4

Raíces cuadradas y valores absolutos
b² = a
(3)² = 9
así que b = 3
pero!!!
(-3)² = 9 de tal manera que b = -3

La raíz cuadrada positiva del cuadrado de un número es igual a dicho número.

Teorema 1.2.2
Para cualquier número real a
√a² = |a|
p.ej.
√(-4)² = √16 = 4 = |-4|

Teorema 1.2.3
Si a y b son números reales, entonces,

|-a| = |a| el número a y su negativo tienen los mismos valores absolutos.
|ab| = |a||b| El valor absoluto de un producto es igual al producto de los valores absolutos.
|a/b| = |a|/|b| El valor absoluto de una relación es igual a la relación de los valores absolutos.

Demostración

Del teorema 1.2.2

(a) |-a| = √(-a)² = √a² = |a|

(b) |ab| = √(ab)² = √a²b² = √a²√b² = |a||b|

Ejemplos

(a) |-4| = |4|

(b) |2.-3| = |-6| = 6 = |2|.|3| = 6

(c) |5/4| = 5/4 = |5|/|4| = 5/4

El resultado (b) del teorema anterior puede extenderse a tres o más factores.
Para múltiples números reales
a₁, a₂, a₃,...a_n
(a) |a₁ a₂ ...a_n| = |a₁| |a₂| ...|a_n|
(b) |aⁿ| = |a|ⁿ

Interpretación geométrica del valor absoluto.

Donde A y B son puntos con coordenadas a y b. La distancia entre A y B es
$\text{distancia}=\begin{cases}b-a \ \ \text{ si } a < b \\ a-b \ \ \text{ si } a > b \\ 0 \ \ \text{ si } a = b \end{cases}$

Teorema 1.2.4 (Fórmula de distancia)

Si A y B son puntos en una línea de coordenadas con coordenadas a y b respectivamente, entonces la distancia d entre A y B
d = |b - a|

Tabla 1.2.2 (a)

|x-a| < k (k>0)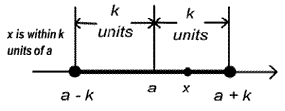

Forma alternativa -k < x-a < k
La solución queda (a-k, a+k)

Ejemplo

La desigualdad
|x-3| < 4
reescrita como
-4 < x-3 < 4
añadiendo 3 a lo largo resulta
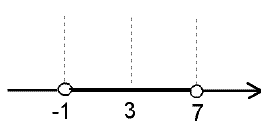
-1 < x < 7
La solución queda (-1,7)

Sobre la linea real

Ejemplo

Resuelva |x+4| ≥ 2

x+4 ≤ -2
x ≤ -6

x+4 ≥ 2
x≥ -2

Al combinar estos dos arreglos de ecuaciones resulta
(-∞ , -6] ∪ [-2 , +∞ )

Sobre la línea real

La Desigualdad del triángulo

No es generalmente cierto que
|a+b| = |a| + |b|
p.ej.
si a = 2 y b = -3, entonces a+b = -1 de tal manera que |a+b| = |-1| = 1
mientras
|a|+|b| = |2|+|-3| = 2+3 = 5 entonces |a+b| = |a|+|b|

1.2.5 Teorema - (La desigualdad del triángulo)

Si a b entonces |a+b| ≤ |a|+|b|

Demostración

Dado que cualesquiera números a y b, sabemos que
-|a| ≤ a ≤ |a| y -|b| ≤ b ≤ |b|
-|a| ≤ a ≤ |a|
+
-|b| ≤ b ≤ |b|
______________
= -|a| + -|b| ≤ a+b ≤ |a|+|b|
______________________________________________
Ahora tenemos dos casos:

Caso 1 donde a+b ≥ 0
ciertamente a+b=|a+b|
Por lo tanto
|a+b| ≤ |a|+|b|

y

Caso 2 donde a+b < 0
|a+b| = -(a+b)
o
(a+b) = -|a+b|

Comparando con la desigualdad inicial
-(|a|+|b|) ≤ -|a+b|
El resultado sigue
←^{_______________________________}→