Follow @Math10_com

Trigonometry - sin, cos, tan, cot

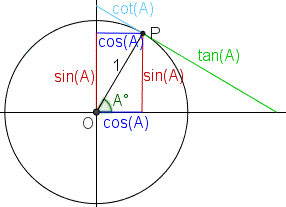
Take an x-axis and an y-axis (orthonormal) and let O be the origin. A circle centered in O and with radius = 1 is known as trigonometric circle or unit circle.

If P is a point from the circle and t is the angle between PO and x then:

the x-coordinate of P is called the cosine of t. We write cos(t);
the y-coordinate of P is called the sine of t. We write sin(t);
the number sin(t)/cos(t) is called the tangent of t. We write tan(t);
the number cos(t)/sin(t) is called the cotangent of t. We write cot(t).

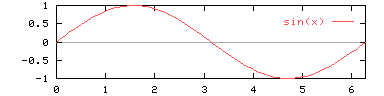
The sine function

sin : R -> R
All trygonometric functions are periodic. The period of sin is 2π.
The range of the function is [-1,1].

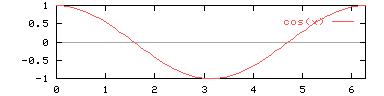
The cosine function

cos : R -> R
The period of sin is 2π.
The range of the function is [-1,1].

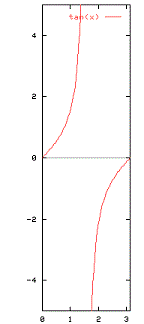
The tangent function

tan : R -> R
The range of the function is R. Now, the period is π and the function is undefined at x = (π/2) + kπ, k=0,1,2,...

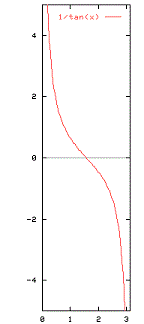
The cotangent function

cot : R -> R
The range of the function isR. The period is π and that the function is undefined at x = kπ, k=0,1,2,...

The values of sin, cos, tan, cot at the angles of 0°, 30°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°

$\alpha^o$	$0^o$	$30^o$	$45^o$	$60^o$	$90^o$	$120^o$	$135^o$	$150^o$	$180^o$	$210^o$	$225^o$	$240^o$	$270^o$	$300^o$	$315^o$	$330^o$	$360^o$
$\alpha rad$	$0$	$\frac{\pi}{6}$	$\frac{\pi}{4}$	$\frac{\pi}{3}$	$\frac{\pi}{2}$	$\frac{2\pi}{3}$	$\frac{3\pi}{4}$	$\frac{5\pi}{6}$	$\pi$	$\frac{7\pi}{6}$	$\frac{5\pi}{4}$	$\frac{4\pi}{3}$	$\frac{3\pi}{2}$	$\frac{5\pi}{3}$	$\frac{7\pi}{4}$	$\frac{11\pi}{6}$	$2\pi$
$sin\alpha$	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$	$-\frac{1}{2}$	$-\frac{\sqrt{2}}{2}$	$-\frac{\sqrt{3}}{2}$	$-1$	$-\frac{\sqrt{3}}{2}$	$-\frac{\sqrt{2}}{2}$	$-\frac{1}{2}$	$0$
$cos\alpha$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$	$-\frac{1}{2}$	$-\frac{\sqrt{2}}{2}$	$-\frac{\sqrt{3}}{2}$	$-1$	$-\frac{\sqrt{3}}{2}$	$-\frac{\sqrt{2}}{2}$	$-\frac{1}{2}$	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$
$tan\alpha$	$0$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$	$-$	$-\sqrt{3}$	$-1$	$-\frac{\sqrt{3}}{3}$	$0$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$	$-$	$-\sqrt{3}$	$-1$	$-\frac{\sqrt{3}}{3}$	$0$
$cot\alpha$	$-$	$\sqrt{3}$	$1$	$\frac{\sqrt{3}}{3}$	$0$	$-\frac{\sqrt{3}}{3}$	$-1$	$-\sqrt{3}$	$-$	$\sqrt{3}$	$1$	$\frac{\sqrt{3}}{3}$	$0$	$-\frac{\sqrt{3}}{3}$	$-1$	$-\sqrt{3}$	$-$

The easiest way to remember the basic values of sin and cos at the angles of 0°, 30°, 60°, 90°:
sin([0, 30, 45, 60, 90]) = cos([90, 60, 45, 30, 0]) = sqrt([0, 1, 2, 3, 4]/4)

Trigonometric identities

With t radians corresponds exactly one point P(cos(t),sin(t)) on the unit circle. The square of the distance [OP] = 1. Calculating this distance with the coordinates of P we have for each t:

cos²(t) + sin²(t) = 1

If t + t' = 180° then:

sin(t) = sin(t')
cos(t) = -cos(t')
tan(t) = -tan(t')
cot(t) = -cot(t')

If t + t' = 90° then:

sin(t) = cos(t')
cos(t) = sin(t')
tan(t) = cot(t')
cot(t) = tan(t')

$\begin{tabular}{|c|c|c|c|c|} \hline & -\alpha & 90^\circ - \alpha & 90^\circ + \alpha & 180^\circ - \alpha \\ \hline \textrm{ sin } & -\textrm{ sin }\alpha & \textrm{ cos }\alpha & \textrm{ cos } \alpha & \textrm{ sin }\alpha \\ \hline \textrm{ cos } & \textrm{ cos }\alpha & \textrm{ sin }\alpha & -\textrm{ sin} \alpha & -\textrm{ cos }\alpha \\ \hline \textrm{ tan } & -\textrm{ tan }\alpha & \textrm{ cot }\alpha & -\textrm{ cot } \alpha & -\textrm{ tan }\alpha \\ \hline \textrm{ cot } & -\textrm{ cot }\alpha & \textrm{ tan }\alpha & -\textrm{ tan } \alpha & -\textrm{ cot }\alpha \\ \hline \end{tabular}$

Trigonometric formulas

cos(u - v) = cos(u).cos(v) + sin(u).sin(v)
cos(u + v) = cos(u - (-v)) = cos(u).cos(-v) + sin(u).sin(-v)

sin(u - v) = sin(u).cos(v) - cos(u).sin(v)
sin(u + v) = sin(u).cos(v) + cos(u).sin(v)

tan(u + v) =

sin(u + v)

cos(u + v)

sin(u).cos(v) + cos(u).sin(v)

cos(u).cos(v) - sin(u).sin(v)

tan(u + v) =

tan(u) + tan(v)

1 - tan(u).tan(v)

sin(2u) = 2sin(u).cos(u)
cos(2u) = cos²(u) - sin²(u)

tan(2u) =

2tan(u)

1- tan²(u)

cos(2u) =

1 - tan²(u)

1 + tan²(u)

sin(2u) =

2tan(u)

1 + tan²(u)

1 + cos(2u) = 2 cos²(u)
1 - cos(2u) = 2 sin²(u)

Addition and multiplication of sin and cos

$\textrm{ sin } \alpha + \textrm{ sin }\beta = 2 \textrm{ sin }\frac{\alpha + \beta}{2} \textrm{ cos }\frac{\alpha - \beta}{2} \qquad \qquad \qquad \qquad \qquad \qquad \textrm{ sin } \alpha - \textrm{ sin }\beta = 2 \textrm{ sin }\frac{\alpha - \beta}{2} \textrm{ cos }\frac{\alpha + \beta}{2} \\ \textrm{ cos } \alpha + \textrm{ cos }\beta = 2 \textrm{ cos }\frac{\alpha + \beta}{2} \textrm{ cos }\frac{\alpha - \beta}{2} \qquad \qquad \qquad \qquad \qquad \qquad \textrm{ cos } \alpha - \textrm{ cos }\beta = -2 \textrm{ sin }\frac{\alpha + \beta}{2} \textrm{ sin }\frac{\alpha - \beta}{2} \\ \textrm{ sin }\alpha \textrm{ sin }\beta = \frac{1}{2} (\textrm{ cos }(\alpha - \beta) - \textrm{ cos }(\alpha + \beta)) \qquad \qquad \qquad \textrm{ cos }\alpha \textrm{ cos }\beta = \frac{1}{2} (\textrm{ cos }(\alpha - \beta) + \textrm{ cos }(\alpha + \beta)) \\ \textrm{ sin }\alpha \textrm{ cos }\beta = \frac{1}{2} (\textrm{ sin }(\alpha + \beta) + \textrm{ sin }(\alpha - \beta))$

Trigonometric functions plotter

Trigonometry in the math forum

Trigonometry Forum

Send us math lessons, lectures, tests to: