Logarithms, logs, log, ln, lg
Logarithmic series
Maclaurin's series cannot be used to find a series for logx, so another method must be found. The first step, yielding a basic logarithmic series,
f(x) = logεx $f_1(x)=\frac{1}{x}$
Use of f(x) = logε(1+x) $f_1(x)=\frac{1}{1+x}$ f1(0) = 1
f0(x) = logε1 = 0 $f_2(x)=-\frac{1}{(1+x)^2}$ f2(0) = -1
ε0 = 1 $f_3(x)=\frac{2}{(1+x)^3}$ f3(0) = 2
$f_4(x)=\frac{-6}{(1+x)^4}$ f4(0) = -6
$log_{\epsilon}(1+x) = x-\frac{x^2}{2!}+\frac{2x^3}{3!}-\frac{6x^4}{4!}....$
$= x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4!}+\frac{x^5}{5}....$
When the coefficients are simplified by dividing by the factorial number series, they are a sort of harmonic series that doesn't converge very rapidly. Numerators are successive powers of x, and denominators are the simple number series, not the factorial.
You'll want logs of numbers bigger than 2. Here, the rate of convergence is shown in finding log 2 by this method. Two things slow its convergence: the only diminishing factor is essentially a harmonic series of the integral number reciprocals. It straddles the ultimate value, which means it has to converge much further to reach its ultimate value.

Logarithmic series: modified
Here is a trick that logarithms are made for. If you modify the variable again, using (1 + x)/(1 - x), by the principles of logarithms, the log of this variable will be the log of (1 + x) minus the log of (1 - x).
First, the series of log(l - x) was a succession of powers of x divided by the harmonic succession of integral numbers, alternating in sign. The series for log(l - x) uses the same numerical terms, but all the signs are minus. Remember, you're going to subtract it from log(l + x), which turns all those minus signs positive in the final value.
This method does two things: it knocks out the even powers of x and combines them. The series is contained in big parentheses, multiplied by 2.
To show how much more quickly this series converges, use it to calculate log 2, which by the first method would take forever. Make (x + 1)/(x - 1) = 2. That's another variable change. Solving that equation, the variable in the series is not 1, but 1/3. Since every other term has dropped out, successive terms diminish by x (or 1/9). This ratio results in much quicker convergence. It converges so rapidly that only 4 terms are now needed to obtain log 2 to 4 places of decimals.

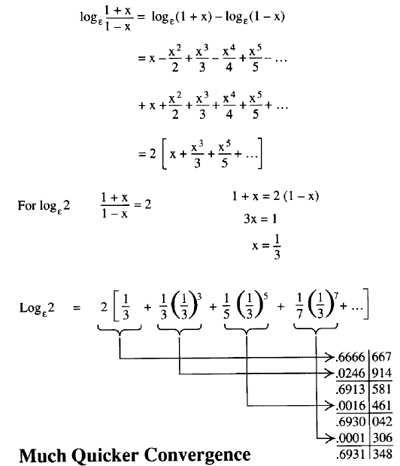
Calculating logarithms
Here you calculate two logarithms to find a comparison in convergence rate. To calculate log 1.1, make x = 1/21. Successive terms now converge by more than 400:1. Three terms of the series produce the log correct to six decimal places.
As you already saw, to calculate log 2, x = 1/3, so convergence is about one decimal place for each extra term. For accuracy to six places, seven terms are required.
Now try log 3; x = 1/2. The series converges much more slowly, but try another way. You've already "done" log 2. Log 3 = log 2 + log 1.5, because 3 = 2.1,5. So, find log 1.5 and add it to log 2. Log 1.5uses x = 1/5 and it converges faster than log 2 did. Now you have a quicker reliable 6-figure value for log 3.


In the example above, you tackle finding all the logs for integers up to 10. Notice the short cuts you can take. Log 4 is twice log 2. You can derive it either from 4 = 2.2 or from 4 = 22. Log 5 is log 4 + log 1.25. Log 6 is log 2 + log 3. Log 7 is log 4 + log 1.75. Log 8 is 3 times log 2 because 8 is 23. Log 9 is twice log 3 because 9 = 32. Finally, log 10 is log 2+ log 5.
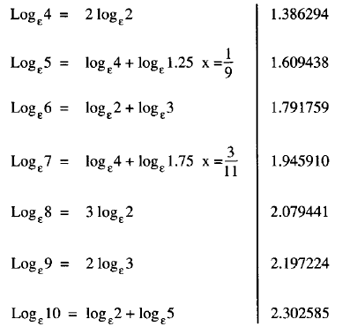
Common logarithms
Although all logarithms must be calculated in their basic form to the base e, sometimes called hyperbolic or Naperian logarithms (from the name of the discoverer of logarithms), they are generally called either natural logarithms or log base e.
Log10x = y x = 10y Logε10 = t εt = 10
So x = (εt)y = εty Logεx = ty
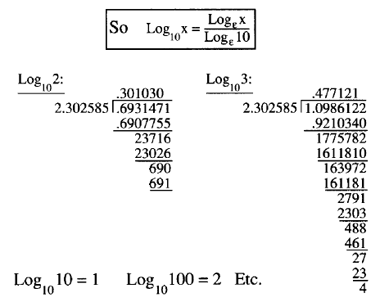
If logs used base 10, then log 10 to base 10 is 1. You change the base by dividing the natural logarithm by log 10. The resulting figure is the same number's logarithm in base 10.
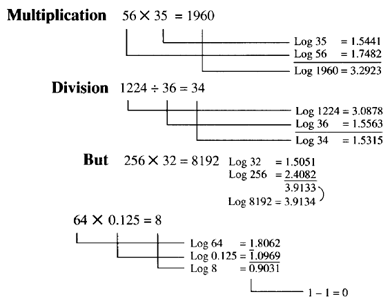
Using logarithms: multiplication and division
Most students of this edition will use logarithms from their pocket calculator- it's so much easier than using tables. A calculator that provides logs has both kinds, natural and common. The key for common logs is marked log and the one for natural logs is marked ln. Both are useful.
The examples here were prepared from 4-figure log tables. Your calculator probably lists more figures than the tables did. On my calculator, I enter log 32 and get 1.505149978; 256 produces 2.408239965. Adding them is 3.9133889944. Using the shift, which reverses the action, the answer is 8192 exactly!
The last example shows another difference with tables. The table only gave the mantissa - the decimal part. You had to insert the characteristic - the whole number to the left of the decimal point that tells where the point is in the number itself. 0.0969 is the mantissa (in 4-figure tables) for the digits 125. The bar over the 1 indicates that the characteristic is negative. So, the log is -1 + 0.0969. My calculator reads -0.903089987. However, if I enter 1.25 instead of 0.125, it reads 0.096910013. If the number is larger than 1, the mantissa doesn't change; only the characteristic changes as the decimal point shifts.
Using logarithms: indices
Here again, the examples on here were prepared from 4-figure tables. A pocket calculator can find the answers far more accurately. In fact, most calculators have one key, xy, which saves the use of the log key altogether. However, just look at here and "work it over" with a calculator.
Log 12reads 1.079181246. x3 makes it 3.23764 3738. Using the shift and log produces 1728 exactly. Enter 12 again. Press xy, then 3, and =. The calculator reads 1728 again.
In the next example, log 2 is 0.301029995, the correct answer again. However, entering log 1024 lists 3.010299957 one more place.
Above are used logs or the xy key where the indices were fairly obvious. Sometimes the answer isn't that simple. Here's one: 354/5. Doing it by calculator logs: Log 35 = 1.544068044. Times 0.8=1.235254435. Shift log= 17.18915135. Using the xy key produces the same answer.
You could also calculate it by binomial expansion and take it further, if your calculator is equipped with adequate memory and paren features. You needn't recalculate each term. After the second term, you can multiply/divide by the additional factors. For example, to get the third term from the second, multiply by 3 and divide by 320, and so on. This series converges very rapidly.


By Binomial Expansion

By Binomial Expansion
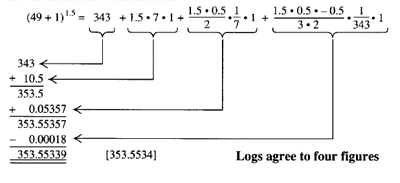
In this one, 4-figure logs are rather limited. Using the same calculator, either with logs or the xy key, the result is 353.5533906. The choice of binomial expression produced all except the last two digits with only 4 terms.
Of course, your calculator won't pick up a binomial series for you. That's just an exercise to show that the binomial works to check your calculating. How does the calculator do it? It has built-in programs that run the log series - so fast it will read an answer in a fraction of a second. Remember, it works in binary, even though it keeps track of decimal digits. It's fast, but you have the brains!
Using logarithms with a formula
The formula here relates pressure and volume in the physical expansion and compression of a true gas. It is typical of many application formulas. The quantities p and v are variable, k and index n are both constants. In this tabulation, k = 1000 and n = 1.4.
Tabulate values of v from 10 to 30 (assuming this covers the range needed in our specific problem) and use logarithms to calculate the corresponding value of p (in the last column). The 3rd column lists values of 0.4 log v as an aid in finding 1.4 log v. Tabulating with this method made the work easier before the advent of calculators.
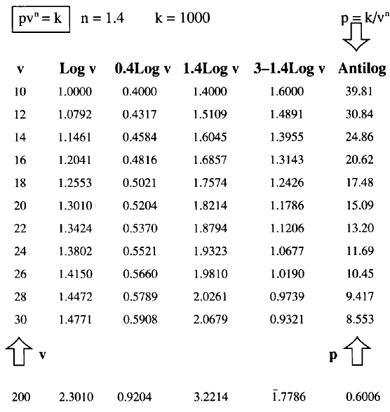
The 4th column subtracts from 3, which is log 1000. To do this on a calculator, you have a choice: use logs or the xy key. Either way, you have a twist to get k into it. If k was other than a power of 10, it would complicate matters a little. One method is to use the 1/x (reciprocal) key, then multiply by 1000 (or whatever k is).
Finding the law by logarithms
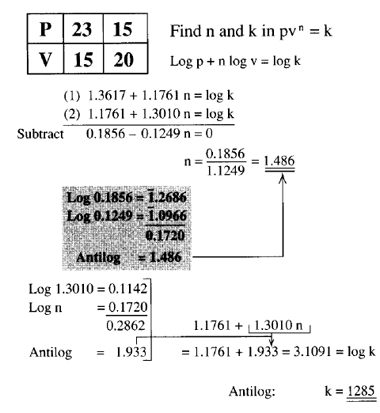
Here, the process of the previous section is reversed. You know that a few pairs of values for v and p relate, according to a law of the type: pvn = k. This shows how it was done by logs, again before the advent of calculators. You can use your calculator here, but the option of using the xy key is not so easy; using the log key is easier.
Take the logs of the p values: 1.361727836 and 1.176091259. Subtract, getting 0.185636579. Take the logs of the v values: 1.176091259 and 1.301029996. Again subtract: 0.124938736. Divide the first subtraction by the second: 0.185636579/0.124938736= 1.485820827, the value for n. This calculation involves use of your calculator's memory or a scratch pad. Realize that all those digits are unnecessarily "accurate." The numbers you began with are probably only accurate to 2 significant figures.
Questions and problems
1. Refer to the following drawing. These functions are graphed on a log-log scale. Redraw approximations of the functions on a semilog scale (with the x axis linear and the y axis logarithmic). Choose scales that are reasonable for the angle of values in each case.
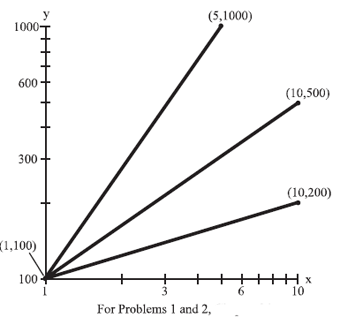
2. Redraw approximations of the functions of the above drawing in rectangular coordinates. Choose scales that are reasonable for the range of values in each case. The scales need not be the same on each axis, but both axes must be linear.
3. Refer to the following drawing. These functions are graphed in rectangular coordinates. Redraw approximations of the functions on a semilog scale (with the x axis linear and the y axis logarithmic). Choose scales that are reasonable for the range of values in each case.
4. Redraw approximations of the functions of the above drawing in log-log coordinates. Choose scales that are reasonable for the range of values in each case. The scales need not be the same on each axis, but both axes must be logarithmic.
5. Using the formula log10xy = log10x + log10y, find the following products by adding numbers. You may use a calculator. Express your answers to three significant digits.
(a) 5.44 • 3.67 (b) 10.5 • 0.567
(c) 36.7 • 2.56 (d) 0.987 • 0.822

6. Using the formula log10xy = ylog10x, find the values of the following expressions to three significant digits. You may use a calculator.
(a) 5.443,67 (b) 10.53,67
(c) 36.72,56 (d) 0.9870,822
7. If natural logs (base-e) were used instead of base-10 logs in the calculations for problem 6, would the results still be valid?
8. If base-7 logs were used rather than base-10 logs in the calculations for problem 6, would the results still be valid?

 MENU
MENU