Trigonometric and Geometric Conversions
List of all trigonometric identities(formulas)
Ratios for sum angles
As the examples showed, sometimes we need angles other than 0, 30, 45, 60, and 90 degrees. In this chapter you need to learn two things:
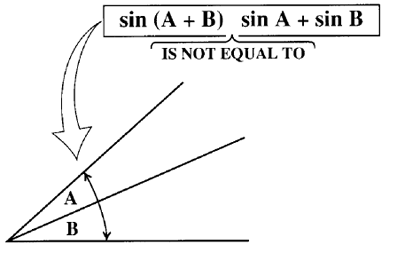
1. Sin(A + B) is not equal to sin A + sin B. It doesn't work like removing the parentheses in algebra.
2. The formula for what sin(A + B) does equal.
First to show that removing parentheses doesn't "work." Here: make A 30 degrees and B 45 degrees.
Sin 30 is 0.5. Sin 45 is 0.7071. Adding the two is 1.2071.
You know that no sine (or cosine) can be more than 1. Why? the ratio has the hypotenuse as its denominator. The most that the numerator can be is equal to the denominator. A sine or cosine can never be greater than 1, so a value of 1.2071 must be wrong.
Wanted sine, cosine, or tangent, of whole angle (A + B)

Finding sin(A + B)
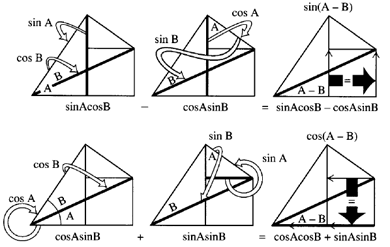
The easiest way to find sin(A + B), uses the geometrical construction shown here. The big angle, (A + B), consists of two smaller ones, A and B, The construction (1) shows that the opposite side is made of two parts. The lower part, divided by the line between the angles (2), is sin A. The line between the two angles divided by the hypotenuse (3) is cos B. Multiply the two together. The middle line is in both the numerator and denominator, so each cancels and leaves the lower part of the opposite over the hypotenuse (4).
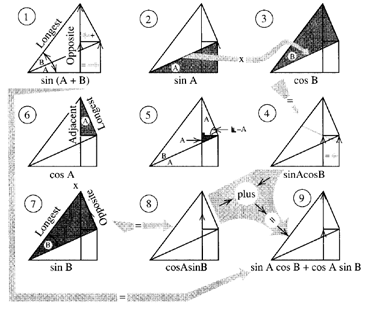
Notice the little right triangle (5). The shaded angle is A, because the line on its top side is parallel to the base line. Similar right triangles with an angle A show that the top angle, marked A, also equals the original A. The top part of the opposite (6), over the longest of that shaded triangle, is cos A. The opposite over the main hypotenuse (7) is sin B. Since the side marked "opposite" (7) is in both the numerator and denominator when cos A and sin B are multiplied together, cos A sin B is the top part of the original opposite — for (A + B) — divided by the main hypotenuse (8).
Now, put it all together (9). Sin(A + B) is the two parts of the opposite - all divided by the hypotenuse (9). Putting that into its trig form:
Finding cos(A + B)
A very similar construction finds the formula for the cosine of an angle made with two angles added together.
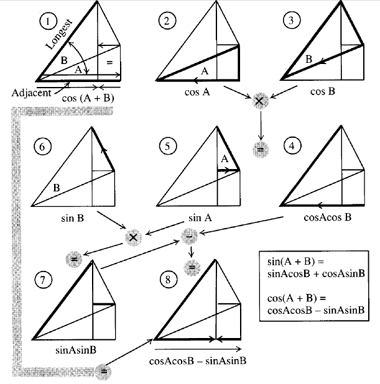
Using the same construction (1), notice that the adjacent side is the full base line (for cos A), with part of it subtracted at the right. Each part must use the same denominator, the hypotenuse of the (A + B) triangle.
The full base line, divided by the dividing line between angles A and E, is cos A (2). This dividing line, divided by the hypotenuse of (A + B) triangle, is cos B (3). So, the full base line divided by the hypotenuse is the product cos A cos B (4).
Now, for the little part that has to be subtracted. The shaded part (5) represents sin A, which multiplied by the shaded part (6) is sin E, which produces the other piece you need (7). The subtraction produces cos(A + B) (8) so that the formula we need is:
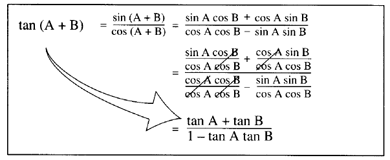
Finding tan(A + B)
A complete geometric derivation of the formula for tan(A + B) is complicated. An easy way is to derive it from the two formulas that you have already done. In any angle, the tangent is equal to the sine divided by the cosine. Using that fact, tan(A + B) = sin(A + B)/cos(A + B). In a way that does it, but you can expand that to:
$\tan(A + B) = \frac{\sin\ A \cos\ B + \cos\ A\ \sin\ B}{\cos\ A \cos\ B - \sin\ A\ \sin\ B}$
Divide through top and bottom by cos A cos B, which turns all the terms into tangents, giving:
$\tan(A + B) = \frac{\tan\ A + \tan\ B}{1 - \tan\ A\ \tan\ B}$

Ratios for 75 degrees
Show the ratios for sine, cosine, and tangent by substituting into the sum formula, then reducing the result to its simplest form, before evaluating the surds. After making the basic substitutions in each case, the rough work is in shading - to show how the result is reduced to the simplest form for evaluation.

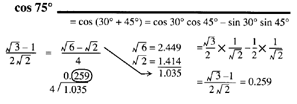
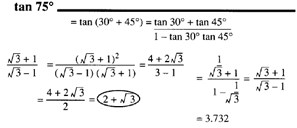
If you use your pocket calculator for evaluation, it will probably make no difference whether you simplify the expressions first or just plow through it! Everything depends on the calculator: some do make a difference, some don't!
Ratios of angles greater than 90 degrees
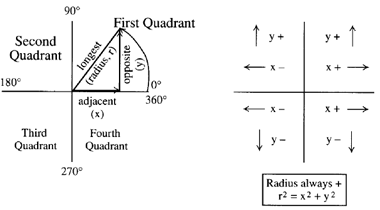
So far, ratios of acute angles (between 0 and 90 degrees) have been considered. Other triangles with obtuse angles (over 90 degrees) might go over 180 degrees in later problems. To simplify classification of angles according to size, they are divided into quadrants.
A quadrant is a quarter of a circle. Since the circle is commonly divided into 360 degrees, the quadrants are named by 90-degree segments. 0-90 degrees is the 1st quadrant, 90-180 the 2nd, 180-270 the 3rd, and 270-360 the 4th.
Drawing in lines to represent the quadrant boundaries, with 0 or 360 horizontal to the right, 90 vertical up, 180 horizontal to the left, and 270 vertical down. Now, use this method for plotting graphs.
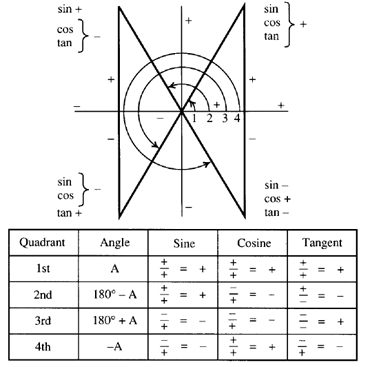
Progressively larger angles are defined by a rotating vector, starting from zero and rotating counterclockwise. Horizontal elements are x: positive to the right, negative to the left. Vertical elements are y. positive up, negative down. The rotating vector is r. So, the sine of an angle is y/r, the cosine x/r, and the tangent y/x. The vector r is always positive. So, the sign of the ratios can be figures for the various quadrants.
Here, the signs of the three ratios have been tabulated for the four quadrants. Also how the equivalent angle in the first quadrant "switches" as the vector passes from one quadrant to the next. In the first quadrant, the sides were defined in the ratios for sine, cosine, and tangent. As you move into bigger angles in the remaining quadrants, the opposite side is always the vertical (y). What was called the adjacent is always the horizontal (x). The hypotenuse is always the rotating vector (r). You will begin to see a pattern to the way these trigonometric ratios for angles vary.
Ratios in the four quadrants
Ratios for difference angles
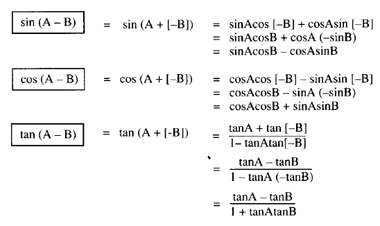
Now, you have two ways to obtain formulas for difference angles. First, use a geometric construction, such as the one that was used for sum angles, reversing it so that (A - B) is the angle B subtracted from the angle A.
In reasoning similar to that which was used for the sum angles, presented here somewhat abbreviated, are the sine and cosine formulas:
and
 Geometrical Construction
Geometrical Construction
Sum and difference formulas
The second method of finding the formula for difference angles uses the sum formula already obtained, but makes B negative. From our investigation of the signs for various quadrants, negative angles from the 1 st quadrant will be in the 4th quadrant. Making this substitution produces the same results that arrived geometrically in the previous section.
Finding the tangent formula follows the same method, either going through substitution into the sine and cosine formulas, or more directly, by making tan(-B) = - tan B. Either way you get:
$\tan(A - B) = \frac{\tan\ A - \tan\ B}{1 + \tan\ A\ \tan\ B}$
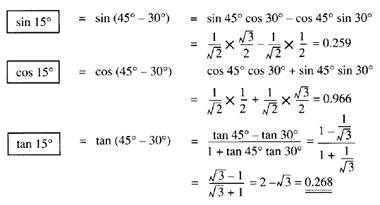
Ratios through the four quadrants
You can deduce a few more ratios with the sum and difference formulas. You already did ratios for 75 degrees. Now, do those for 15 degrees. These formulas give ratios for angles at 15-degree intervals through the four quadrants. Plotting them out for the full 360 degrees, you can see how the three ratios change as the vector sweeps through the four quadrants.
Both the sine and cosine "wave" up and down between +1 and -1. Notice that the "waves" are displaced by 90 degrees, one from the other. This fact becomes important later.
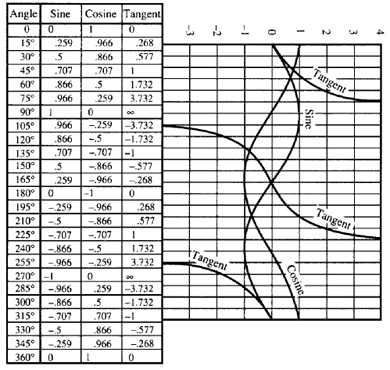
The tangent starts out like the sine curve, but quickly it sweeps up to reach infinity at 90 degrees. Going "offscale" in the positive direction, it "comes on" from the negative direction on the other side of 90 degrees. Going through the 180-degree point, the tangent curve duplicates what it does going through 0 or 360 (whichever you view it as). At 270 degrees, it repeats what it did at 90 degrees.
Pythagoras in trigonometry
A formula can often be simplified, as was found by deriving the tangent formulas from the sine and cosine formulas, and changing it from terms using one ratio to terms using another ratio. In doing this, the Pythagorean theorem, expressed in trigonometry ratios, is very handy.
Assume that a right triangle has a hypotenuse of 1 unit long. Then one of the other sides will have a length of sin A and the other of cos A. From that, the Pythagorean theorem shows that: cos2 A + sin2 A = 1. This statement is always true, for any value of A.
A little thing here about the way it's written. Cos2 A means (cos A)2. If you wrote it cos A2, the equation would mean something else. A is a number in some angular notation that represents an angle. A2 would be the same number squared. Its value would depend on the angular notation used, so it's not a good term to use. What is meant is the angle's sine or cosine squared, not the angle itself.
The Pythagoras formula can be transposed. For instance, two other forms are:
cos2 A = 1 - sin2 A, and sin2 = 1 - cos2 A.

Multiple angles
The sum formulas, along with the Pythagorean theorem, are used for angles that are 2, 3, or a greater exact multiple of any original angle. Here, give formulas for 2A and 3A. The same method is pursued further in Parts 3 and 4 of this book.
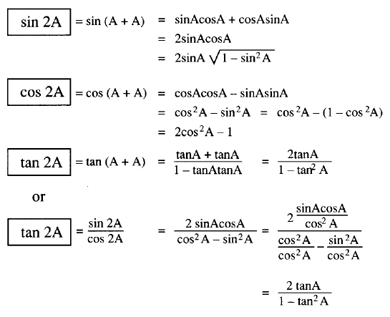
The sum formula works whether both angles are the same or different: sin(A + B) or sin(A + A). However, sin(A + A) is really sin 2A. So, sin 2A is sin A cos A + cos A sin A. They are both the same product, in opposite order, so this statement can be simplified to sin 2A = 2 sin A cos A.
Similarly,
$\tan\ 2A = \frac{2 \tan\ A}{1 - \tan^2 A}$
Now, the triple angle (3A) is used just to show how further multiples are obtained.
Basically, it's as simple as writing 3A = 2A + A and reapplying the sum formulas. But then, to get the resulting formula in workable form, you need to substitute for the 2A part to get everything into terms of ratios for the simple angle A.
Work your way through the three derivations shown here. You can see that it will get more complicated for 4 A and more (in Parts 3 and 4 of this book).
MULTIPLE ANGLES Derived from Sum Formulas
MULTIPLE ANGLES Ratios for 3A

Properties of the isosceles triangle
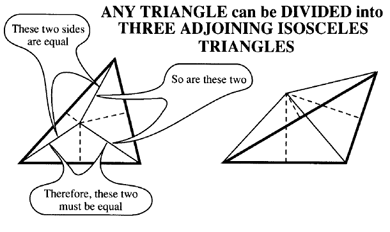
You have already seen that a right triangle is a useful building block for other shapes. An isosceles triangle has slightly different uses. But the fact on which these uses are based is that an isosceles triangle has two equal sides and two equal angles opposite those two sides. A perpendicular from the third angle (not one of the equal ones) to the third side (not one of the equal ones) bisects that third side. That is, it divides it into two equal parts, making the whole triangle into mirror-image right triangles.
With isosceles triangles, any triangle, except a right triangle, can be divided into three adjoining isosceles triangles, by dividing each side into two equal parts and erecting perpendiculars from the points of bisection. Where any two of these bisecting perpendiculars meet, if lines are drawn to the corners of the original triangle, the three lines must be equal, because two of them form the sides of an isosceles triangle. So, the perpendicular from the third side of the original triangle must also meet in the same point.
This statement is true, as we show here, whether the original triangle is acute or obtuse. The difference with an obtuse-angled triangle is that the meeting point is outside the original triangle, instead of inside.
What does a right triangle do? Perpendiculars from the mid-point of the hypotenuse to the other two sides will bisect those two sides - you get two out of three! The meeting point happens to sit on the hypotenuse.

Angles in a circle
A basic property of a circle is that its center is at an equal distance from every point on its circumference. This equal distance is the radius of the circle.
If you draw any triangle inside a circle, the perpendiculars from the mid points of its side will meet at the circle's center and radii from the corners of the triangle will divide it into three isosceles triangles.
Now, if you name the equal pairs of angles in each isosceles triangle, A, A, B, B, C, C, you find that the original triangle has one angle A + B, one angle B + C, and one angle A + C. The three angles total 2A + 2B + 2C. This, you know, adds up to 180 degrees.
In any isosceles triangle, the angle at the apex is 180 degrees minus twice the base angle. Because of the fact deduced in the previous paragraph, 180 - 2A must be the same as 2B + 2C, for example.
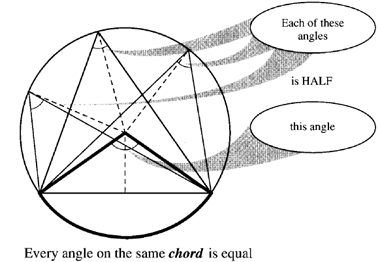
Consider the angles that are opposite from the part of the circle, against which the top left side of the triangle sits. The angle at the centre is 2B + 2C, as just deduced. The angle at the circumference is B + C. "You will find that, for any segment of a circle, the angle at the center is always twice the angle at the circumference.
The proof above leads to an interesting fact about angles in circles. Instead of identifying the angles with a side of a triangle, use an arc (portion of the circumference) of the circle. The important thing is the angle that corresponds to the arc at the center. A part of the circumference of a circle that is identified by the angle at the center is called the chord of the circle.

The angle at the center is twice the angle at the circumference
Any angle drawn touching the circumference, using this chord as termination for the lines bounding the angle, must be just half the angle at the center. Thus, all the angles in a circle, based on the same chord, must be equal. Suppose that the chord has an angle of 120 degrees. The angles at the circumference will all be exactly 60 degrees.
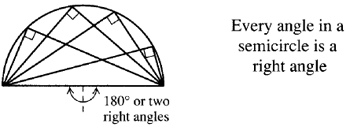
A special case is the semicircle (an exact half circle). The angle at the center is a straight line (180 degrees). Every angle at the circumference of a semicircle is exactly 90 degrees (a right angle). Any triangle in a semicircle is a right triangle.
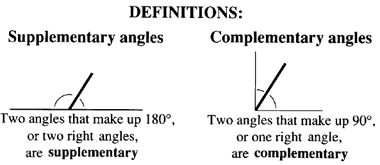
Definitions
Above we have often used angles that add up to either a right angle (90 degrees) or to two right angles (180 degrees). When two angles add up to 180 degrees (two right angles), they are called supplementary. When two angles add up to 90 degrees (one right angle), they are called complementary.
Questions and problems
1. The sine of angle A is 0.8 and the sine of angle B is 0.6. From the various relationships obtained so far, find the following: tan A, tan B, sin(A + B), cos(A + B), sin(A - B), cos(A - B), tan(A + B), and tan(A - B), without using tables or a calculator's trig buttons.
2. At the equator, Earth has a radius of 4000 miles. Angles around the equator are measured in meridians of longitude, with a north-to-south line through Greenwich, England as the zero reference. Two places are used to observe the moon: one is Mt. Kenya, on the equator at 37.5 east of Greenwich; the other is Sumatra, on the equator, at 100.5 east. How far apart are these two places, measured by an imaginary straight line through the Earth?
3. If sights were made horizontally from the observation points in question 2 (due east from the first, due west from the second), at what angle would the lines of sight cross?
4. At a certain time, exactly synchronized at both places, a satellite is observed. In Kenya, the elevation of a line of sight, centered on the satellite, is 58 degrees above horizontal, eastward. In Sumatra, the elevation is 58 degrees above horizontal, westward. How far away is the satellite? Use the distance between the points calculated in question 2.
5. The cosine of a certain angle is exactly twice the sine of the same angle. What is the tangent of this angle? You don't need either tables or calculator for this question.
6. The sine of a certain angle is exactly 0.28. Find the cosine and tangent without tables or the trig functions on your calculator.
7. The sine of a certain angle is 0.6. Find the sine of twice this angle and three times this angle.
8. Find the sine and cosine of an angle exactly twice that of question 7.
9. Using 15 degrees as a unit angle, and the formulas for ratios of 2A and ?>A, find the values of the sines of 30 and 45 degrees.
10. Using 30 degrees as a unit angle, find the values for the sines of 60 and 90 degrees.
11. Using 45 degrees as a unit angle, find values for the tangents of 90 and 135 degrees.
12. Using 60 degrees as a unit angle, find values for the cosines of 120 and 180 degrees.
13. Using 90 degrees as a unit angle, find values for the cosines of 180 and 270 degrees.
14. Using the tangent formulas for multiple angles and the tables, find the tangents for three times 29, 31, 59, and 61 degrees. Account for the changes in sign between three times 29 and 31 degrees and between 59 and 61 degrees.
15. The sine of an angle is 0.96. Find the sine and cosine for twice the angle.
16. A problem leads to an algebraic expression of the form 8cos2 A + cos A = 3. Solve for cos A, and state in which quadrant the angle representing each solution will come. Give approximate values from tables or your calculator.

 MENU
MENU