Measuring Angles

When two lines intersect, they give rise to four different spaces with respect to the point of intersection.
The spaces created are called angles.

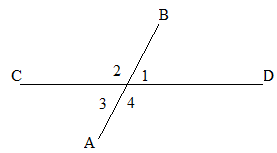
The figure shows 4 different angles formed at the intersection of the two lines AB and CD

Angles are commonly measured in degrees denoted as °. When an object moves through a complete cycle, that is from point D through B, C, A then back to D, we say it has covered 360 degrees (360°). Therefore a degree is $\frac{1}{360}$ of a cycle.

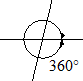
Angles greater than 360 degree

We have discussed that when an object makes one complete cycle around a point, it covers 360°, however, when an object makes more than one cycle, it makes an angle greater than 360 degrees. This is a common occurrence in day to day life. A tire makes numerous cycles when a vehicle is being driven hence; it makes an angle greater than 360°.

To find out the number of cycles made when an object rotates, we count the number of times 360 can be added to it to get a number equal to or less than the angle given. Likewise, we find the number than can be multiplied by 360 to get a number less than but closer to the angle given.

Example 2
1. Find out the number of cycles made when an object makes an angle of
a) 380°
b) 770°
c) 1000°
Solution
a) 380 = (1 × 360) + 20
The object makes one cycle and 20°
Since $20^{\circ} = \frac{20}{360} = \frac{1}{18}$ cycles
The object makes $1\frac{1}{18}$ cycles.

b) 2 × 360 = 720
770 = (2 × 360) + 50
The object makes two cycles and 50°
$50^{\circ} = \frac{50}{360} = \frac{5}{36}$ cycles
The object makes $2\frac{5}{36}$ cycles
c)2 × 360 = 720
1000 = (2 × 360) + 280
$280^{\circ} = \frac{260}{360} = \frac{7}{9}$ cycles
The object makes $2\frac{7}{9}$ cycles

Positive and negative angles

The figure below shows the sign of an angle measured from a common line, 0 degree line

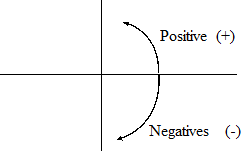
When an object rotates in an clockwise direction, it makes a negative angle of rotation while when it rotates in anticlockwise direction, it makes a positive angle. So far, in our discussions, we have been looking at positive angles only.

In diagram form, a negative angle can be as shown below.

This implies that given a negative angle, we can get its respective positive angle.
For instance, the bottom part of the vertical line is 270°. When measured in the negative direction its will be -90°. We simply subtract 270 from 360. Given a negative angle, we add 360 to get its corresponding positive angle.
When an angle is -360°, it implies that the object made more than one cycle in clockwise direction.

Example 3
1. Find the corresponding positive angle of
a) -35°
b) -60°
c) -180°
d) - 670°

2. Find the corresponding negative angle of 80°, 167°, 330°and 1300°.
Solution
1. We add 360 to the angle to get its corresponding positive angle.
a) -35°= 360 + (-35) = 360 - 35 = 325°
b) -60°= 360 + (-60) = 360 - 60 = 300°
c) -180°= 360 + (-180) = 360 - 180 = 180°
d) -670°= 360 + (-670) = -310
That is one cycle in clockwise direction (360)
360 + (-310) = 50°
The angle is 360 + 50 = 410°

2. We subtract 360 from the angle to get its corresponding negative angle.
80° = 80 - 360 = - 280°
167° = 167 - 360 = -193°
330° = 330 - 360 = -30°
1300° = 1300 - 360 = 940 (one cycle made)
940 - 360 = 580 (second cycle made)
580 - 360 = 220 (third cycle made)
220 - 360 = -140°
The angle is -360 - 360 - 360 - 140 = -1220°
Thus 1300° = -1220°

Radian

A radian is an angle made at the center of circle by an arc which is equal to the length of the radius of that particular circle. It is therefore a unit that is used to measure an angle. The angle is approximately to 57.3°.
In most cases, it is denoted by rad.
Thus $1 rad \approx 57.3^{\circ}$

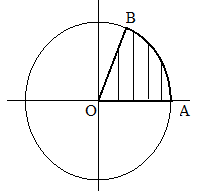
Radius = r = OA = OB = AB
Angle BOA is equal to 1 radians

Since a circumference is given by $2\pi r$ or $2\pi$ radius, hence there are $2\pi$ radians in one complete cycle.

Radians are commonly given in terms of $\pi$ to avoid dealing with decimals in calculations. In most books, the abbreviation rad is not provided, but the reader has to know that when talking about an angle that is given in terms of $\pi$, the units are automatically radians.

Some basic angles in radians:

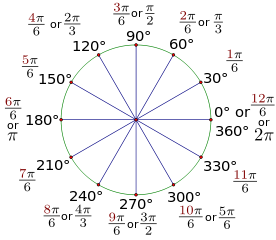
$360^{\circ} = 2\pi\ rad$
$180^{\circ} = \pi\ rad$
$90^{\circ} = \frac{\pi}{2} rad$

$30^{\circ} = \frac{30}{180}\pi = \frac{\pi}{6} rad$

$45^{\circ} = \frac{45}{180}\pi = \frac{\pi}{4} rad$

$60^{\circ} = \frac{60}{180}\pi = \frac{\pi}{3} rad$

$270^{\circ} = \frac{270}{180}\pi = \frac{27}{18}\pi = 1\frac{1}{2}\pi\ rad$

Example 4
1. Convert 240°, 45°, 270°, 750° and 390° into radians in terms of $\pi$.
Solution
We multiply the angles by $\frac{\pi}{180}$.

$240^{\circ} = 240 \times \frac{\pi}{180} = \frac{4}{3}\pi=1\frac{1}{3}\pi$

$120^{\circ} = 120 \times \frac{\pi}{180} = \frac{2\pi}{3}$

$270^{\circ} = 270 \times \frac{1}{180}\pi = \frac{3}{2}\pi=1\frac{1}{2}\pi$

$750^{\circ} = 750 \times \frac{1}{180}\pi = \frac{25}{6}\pi=4\frac{1}{6}\pi$

$390^{\circ} = 390 \times \frac{1}{180}\pi = \frac{13}{6}\pi=2\frac{1}{6}\pi$

2. Convert the following angles into degrees.
a) $\frac{5}{4}\pi$
b) $3.12\pi$
c) 2.4 radians
Solution
$180^{\circ} = \pi$
a) $\frac{5}{4} \pi = \frac{5}{4} \times 180 = 225^{\circ}$
b) $3.12\pi = 3.12 \times 180 = 561.6^{\circ}$
c) 1 rad = 57.3°
$2.4 = \frac{2.4 \times 57.3}{1} = 137.52$

Negative angles and angles greater than $2\pi$ radians

To convert a negative angle to a positive, we add $2\pi$ to the it.
To convert a positive angle to a negative, we subtract $2\pi$ from the it.

Example 5
1. Convert $-\frac{3}{4}\pi$ and $-\frac{5}{7}\pi$ to positive angles in radians.

Solution
We add $2\pi$ to the angle
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$

When an object rotates through an angle that is greater than $2\pi$; it would have made more than one cycle.
To determine the number of cycles of such angle, we find a number when multiplied by $2\pi$, the result is equal or less but closer to the number.

Example 6
1. Find the number of cycles made when an objects rotates through the following angles
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$

Solution
a) $-10\pi = 5(-2\pi)$; since $-2\pi$ implies one cycle in clockwise direction, it implies that
the object made 5 cycles in the clockwise direction.

b) $9\pi = 4(2\pi) + \pi$, $\pi =$ half cycle
the object made four and half cycles in the anticlockwise directions

c) $\frac{7}{2}\pi=3.5\pi=2\pi+1.5\pi$, $1.5\pi$ is a three quarter cycle $(\frac{1.5\pi}{2\pi}=\frac{3}{4})$
the object made one and three quarter cycles in anticlockwise direction