Law of sines, cosines and tangents

Law of sines

The area of a triangle ABC is given by the formulas:

$A = \frac{a\times c \times \sin(B)}{2} = \frac{b \times c \times \sin(A)}{2} = \frac{a \times b \times \sin(C)}{2}$

$a\times c \times \sin(B) = b\times c \times \sin(A) = a \times b \times \sin(C)$

dividing by $a\times b\times c$, we get the sine formula:

$\frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}$

Let R be the radius of a circle with center O through points A,B and C(for every 3 points that do not lie on a straight line there is exactly 1 circle through these points) of a triangle ABC.

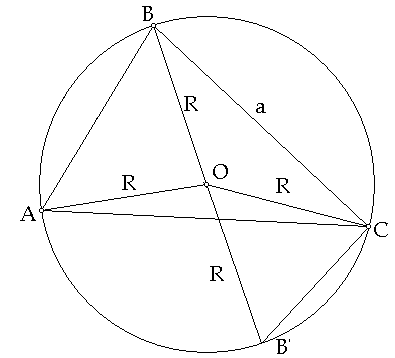
Let B' be the second intersection point of BO and the circle. The
angle B' in the triangle BB'C is equal to A, and the triangle BB'C is a right triangle
=> a = 2Rsin(B') = 2Rsin(A) therefore:

$\frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}=2R$

Law of cosines

Let a(the length of BC), b(the length of CA), c(the length of AB) be the lengths of the sides of a triangle ABC.

a² = b² + c² - 2bc cos(∠A)
b² = c² + a² - 2ca cos(∠B)
c² = a² + b² - 2ab cos(∠C)

Law of tangents

$\frac{a-b}{a+b}=\frac{ \tan\left[\frac{1}{2}(A - B)\right] }{ \tan\left[\frac{1}{2}(A + B)\right] }$

$\frac{b-c}{b+c}=\frac{ \tan\left[\frac{1}{2}(B - C)\right] }{ \tan\left[\frac{1}{2}(B + C)\right] }$

$\frac{a-c}{a+c}=\frac{ \tan\left[\frac{1}{2}(A - C)\right] }{ \tan\left[\frac{1}{2}(A + C)\right] }$

Problems

Sine rule problems
Cosine rule problems