Midline and Midsegment of Trapezoid and Triangle

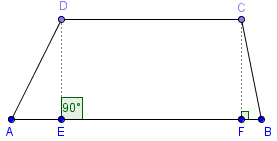
The parallel sides of the trapezoid, are called bases (AB and CD) and the ones that are not parallel are called legs (AD and BC).
If the legs are equal in length, the trapezoid is called isosceles.
DE and CF are altitudes.

Midline of Trapezoid

A line that joins the midpoints of the sides that are not parallel is called a midline(or a midsegment) of trapezoid.

The line MN is the midline of ABCD. And the segment MN is the midsegment of ABCD.

AM = MD
BN = NC

The midline of a trapezoid is parallel to its sides.
In our case - MN || AB || DC.

Theorem 1:

Theorem 2:

In other words:
$\overline{MN} = \frac{\overline{AB} + \overline{DC}}{2}$

Midsegment of a Triangle

The segment that joins the midpoints of two sides of a triangle is called a midsegment of a triangle.

It is parallel to the third side and its length is half as long as the third side.

Theorem: If a line segment crosses the middle of one side of a triangle and is parallel to another side of the same triangle, then this line segment halves the third side.

$\overline{AM} = \overline{MC}$ and $\overline{BN} = \overline{NC}$ =>

$MN || AB$
$\overline{MN} = \frac{\overline{AB}}{2}$

Application of the properties of the midsegments

Divide a segment into equal segments without measuring.

Assignment: Divide a given segment $\overline{AB}$ into 5 equal segments without measuring.

Solution:

Let p be an arbitrary ray with origin A and that does not lie on AB. We draw consecutively five equal segments on p.
$\overline{AA_1} = \overline{A_1A_2} = \overline{A_2A_3} = \overline{A_3A_4} = \overline{A_4A_5}$
We connect A₅ with B and draw lines through A₄, A₃, A₂ and A₁ that are parallel to A₅B.

They cross AB at points B₄, B₃, B₂ and B₁, respectively. These points divide the segment $\overline{AB}$ into five equal segments.

Indeed, from the trapezoid BB₃A₃A₅ we see that $\overline{BB_4} = \overline{B_4B_3}$. By the same way, from the trapezoid B₄B₂A₂A₄, we obtain $\overline{B_4B_3} = \overline{B_3B_2}$

While from the trapezoid B₃B₁A₁A₃,
$\overline{B_3B_2} = \overline{B_2B_1}$.
Then, from B₂AA₂, it follows that $\overline{B_2B_1} = \overline{B_1A}$. We finally get:
$\overline{AB_1} = \overline{B_1B_2} = \overline{B_2B_3} = \overline{B_3B_4} = \overline{B_4B}$

It is clear that if AB must be divided into another number of equal segments, we must project the same number of equal segments on p. Then we proceed the same way.