Area Formulas
The standard notation for area is A.
Square
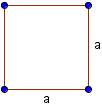
The area of a square of side a is:
Rectangle

If a is the length and b is the width of a rectangle its area is:
Parallelogram
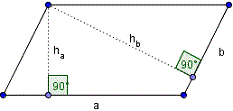
Let a pair of adjacent sides of the palellogram be a and b
and altitudes ha and hb.
The parallelogram area is given by the formula:
Trapezoid

Let the lengths of the both parallel sides of a trapezoid be a and b and the
distance between them is h(the trapezoid altitude).
The area is given by the formula:
Area of a circle
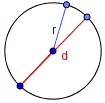
$A = \pi\cdot r^2$
Area of a right triangle
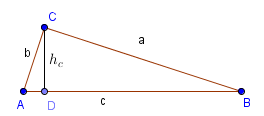
$A=\frac{a\cdot b}{2}$
$A=\frac{c\cdot h_c}{2}$
Area of a triangle
Let ABC be a triangle

with sides of length a, b, c and
altitudes ha, hb and hc.
Area of a triangle by 3 sides
$A = \sqrt{p(p - a)(p - b)(p - c)}$, where $p = \frac{a + b + c}{2}$
The formula is known as Heron's formula, and $p$ is called semiperimeter.
If we exclude the semiperimeter ($p$) the formula looks like:
$A=\frac14\sqrt{4a^2b^2-(a^2+b^2-c^2)^2}$
Area calculator
Enter the triangle:Other formulas for area of a triangle
$A = \frac{a\cdot b\cdot \sin C}{2} = \frac{a\cdot c\cdot \sin B}{2} = \frac{b\cdot c\cdot \sin A}{2}$
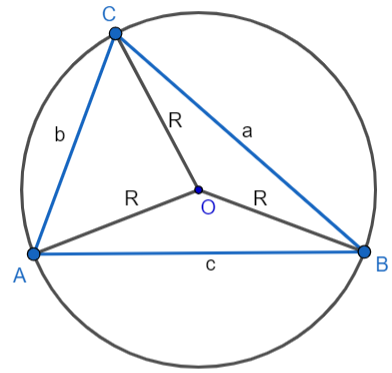
$A = R^2\sin(A) \cdot \sin(B) \cdot \sin(C) = \frac{abc}{4R}$
where R is the radius of the circumscribed circle.
Area of parallelogram, rhombus
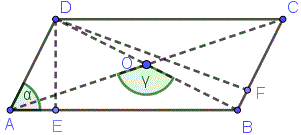
$A = AB\cdot DE = BC \cdot DF$
$A = AB \cdot AD \sin \alpha$
$A = \frac12 AC \cdot BD \sin \gamma$
Area of a quadrilateral

$A = \frac12 AC \cdot BD \sin \varphi $
Area of a regular polygon

$A = \frac14 n\cdot a^2 cot(\frac{\pi}{n})$
n is the number of edges(vertices).
$\pi=3.14159265359$

 MENU
MENU