Formulas from plane analytic geometry

Distance $d$ between two points $P_1(x_1 \textrm{ , } y_1)$ and $P_2(x_2 \textrm{ , } y_2)$

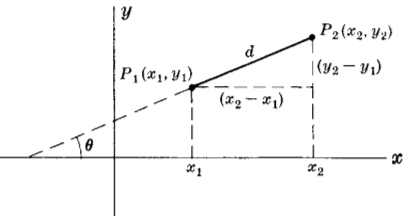
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Slope $m$ of line joining two points $P_1(x_1 \textrm{ , } y_1)$ and $P_2(x_2 \textrm{ , } y_2)$

$m = \frac{y_2 - y_1}{x_2 - x_1} = \textrm { tan } \theta$

Equation of line joining two points $P_1(x_1 \textrm{ , } y_1)$ and $P_2(x_2 \textrm{ , } y_2)$

$\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - y_1} = m$   or   $y - y_1 = m(x - x_1) \\ y = mx + b$
where $b = y_1 - mx_1 = \frac{x_2y_1 - x_1y_2}{x_2 - x_1}$ is the intercept on the $y$ axis, i.e. $y$ intercept.

Equation of line in terms of $x$ intercept $a \ne 0$ and $y$ intercept $b \ne 0$

$\frac{x}{a} + \frac{y}{b} = 1$

Normal form for equation of line

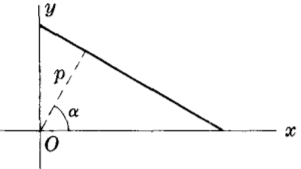
$x \textrm{ cos } \alpha + y \textrm{ sin } \alpha = p$
where $p$ = perpendicular distance from origin $O$ to line
and $\alpha$ = angle of inclination of perpendicular with with positive $x$ axis.

General equation of line

$Ax + By + C = 0$

Distance from point $(x_1 \textrm{ , } y_1)$ to line $Ax + By + C = 0$

$\frac{Ax_1 + By_1 + C}{\pm \sqrt{A^2 + B^2}}$
where the sign is chosen so that the distance is nonnegative.

Angle $\psi$ between two lines having slopes $m_1$ and $m_2$

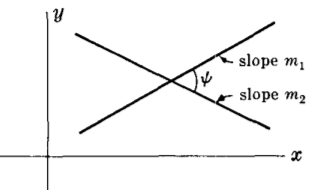
$\textrm{ tan } \psi = \frac{m_2 - m_1}{1 + m_1m_2}$
Lines are parallel or coincident if and only if $m_1 = m_2$
Lines are perpendicular of and only if $m_2 = -\frac{1}{m_1}$

Area of triangle with vertices at $(x_1 \textrm{ , } y_1) \textrm{ , } (x_2 \textrm{ , } y_2) \textrm{ , } (x_3 \textrm{ , } y_3)$

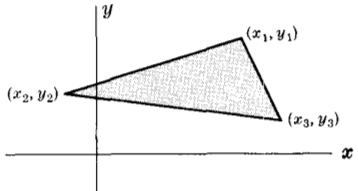
Area
$ = \pm \frac{1}{2} \left| \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array} \right|$
$= \pm \frac{1}{2} ( x_1y_2 + x_2y_3 + x_3y_1 - x_1y_3 - x_2y_1 - x_3y_2 )$
where the sign is chosen so that the area is nonnegative. If the area is zero the points all lie on a line.