SPECIAL PLANE CURVES

LEMNISCATE
Equation in polar coordinates:
$r^2=a^2\cos2\theta$

Equation in rectangular coordinates:
$(x^2+y^2)^2=a^2(x^2-y^2)$

Angle between $AB'$ or $A'B$ and $x$ axis $= 45^\circ$

Area of one loop $=\frac{a^2}{2}$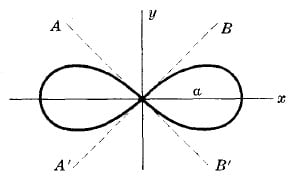

CYCLOID
Equations in parametric form:
$\left\{\begin{array}{lr}x=a(\phi-\sin\phi)\\ y=a(1-\cos\phi)\end{array}\right.$

Area of one arch $=3\pi a^2$

Arc length of one arch $=8a$

This is a curve described by a point $P$ on a circle of radius $a$ rolling along $x$ axis.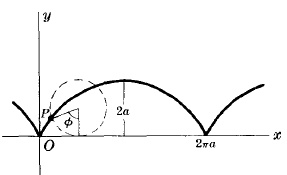

HYPOCYCLOID WITH FOUR CUSPS
Equation in rectangular coordinates:
$x^\frac{2}{3}+y^\frac{2}{3}=a^\frac{2}{3}$

Equations in parametric form:
$\left\{\begin{array}{lr}x=a\cos^3\theta\\ y=a\sin^3\theta\end{array}\right.$

Area bounded by curve $=\frac{3\pi a^2}{8}$

Arc length of entire curve $=6a$

This is a curve described by a point $P$ on a circle of radius $\frac{a}{4}$ as it rolls on the inside of a circle of radius $a$.

CARDIOID
Equation: $r=a(1+\cos\theta)$

Area bounded by a curve $=\frac{3\pi a^2}{2}$

Arc length of a curve $=8a$

This is the curve described by a point $P$ of a circle of radius $a$ as it rolls on the outside of a fixed circle of radius $a$.The curve is also a special case of the limacon of Pascal.

CATENARY
Equation:
$y=\frac{a(e^\frac{x}{a}+ e^{-\frac{x}{a}})}{2}=a\cosh\frac{x}{a}$

This is a curve in which a heavy uniform chain would hang if suspended vertically from fixed points $A$ and $B$.

THREE-LEAVED ROSE
Equation: $r=a\cos3\theta$

The equation $r=a\cos3\theta$ is a similar curve obtained by rotating the curve counterclockwise $30^o$ or $\frac{\pi}{6}$ radians.

In general $r=a\cos n\theta$ or $r=a\sin n\theta$ has $n$ leaves if $n$ is odd.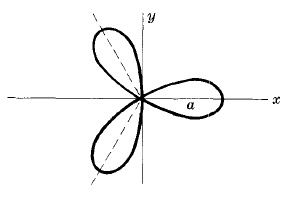

FOUR-LEAVED ROSE
Equation: $r=a\cos2\theta$

The equation $r=a\sin2\theta$ is a similar curve obtained by rotating the curve counterclockwise through $45^o$ or $\frac{\pi}{4}$ radians.

In general $r=a\cos n\theta$ or $r=a\sin n\theta$ has $2n$ leaves if $n$ is even.

EPICYCLOID
Parametric equations:
$\left\{\begin{array}{lr}x=(a+b)\cos\theta-b\cos\left(\frac{a+b}{b}\right)\theta\\ y=(a+b)\sin\theta-b\sin\left(\frac{a+b}{b}\right)\theta\end{array}\right.$

This is a curve described by a point $P$ on a circle of a radius $b$ as it rolls on the outside of a circle of radius $a$.The cardioid is a special case of an epicycloid.

GENERAL HYPOCYCLOID
Parametric equations:
$\left\{\begin{array}{lr}x=(a-b)\cos\phi+b\cos\left(\frac{a-b}{b}\right)\phi\\ y=(a-b)\sin\phi-b\sin\left(\frac{a-b}{b}\right)\phi\end{array}\right.$

This is a curve described by a point $P$ on a circle of a radius $b$ as it rolls on the outside of a circle of radius $a$.

If $b = \frac{a}{4}$, the curve is hypocycloid with four cusps.

TROCHOID
Parametric equations:
$\left\{\begin{array}{lr}x=a\phi-b\sin\phi\\ y=a-b\cos\phi\end{array}\right.$

This is a curve described by a pint $P$ at distance $b$ from the center of a circle of radius $a$ as the circle rolls on the $x$ axis.
If $b < a$, the curve is as shown on Fig.11-10 and is called curtate cycloid.
If $b > a$, the curve is as shown on Fig.11-11 and is called a prolate cycloid.
If $b = a$, the curve is a cycloid.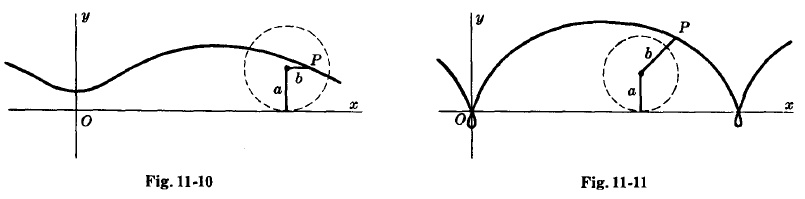

TRACTRIX
Parametric equations:
$\left\{\begin{array}{lr}x=a(\ln\cot\frac{1}{2}\phi-\cos\phi)\\ y=a\sin\phi\end{array}\right.$

This is a curve described by endpoint $P$ of a taut string $PQ$ of length $a$ as the other end $Q$ is moved along the $x$ axis.

WHITCH OF AGNESI
Equation in rectangular coordinates: $y=\frac{8a^3}{x^2+4a^2}$

Parametric equations:
$\left\{\begin{array}{lr}x=2a\cot\theta\\ y=a(1-\cos2\theta)\end{array}\right.$

In the figure the variable line $OA$ intersects $y = 2a$ and the circle of radius $a$ with center $(0,a)$ at $A$ and $B$ respectively. Any point $P$ on the "which" is located by constructing lines parallel to the $x$ and $y$ axes through $B$ and $A$ respectively and determining the point $P$ of intersection.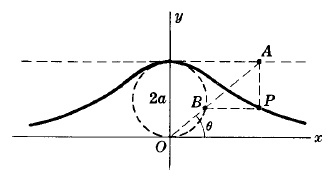

FOLIUM OF DESCARTES
Equation in rectangular coordinates:
$x^3+y^3=3axy$

Parametric equations:
$\left\{\begin{array}{lr}x=\frac{3at}{1+t^3}\\ y=\frac{3at^2}{1+t^3}\end{array}\right.$

Area of loop $\frac{3a^2}{2}$

Equation of asymptote: $x + y + a = 0$.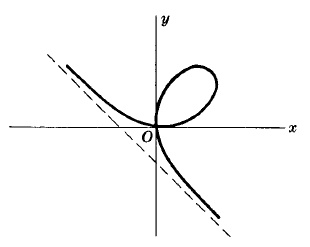

INVOLUTE OF A CIRCLE
Parametric equations:
$\left\{\begin{array}{lr}x=a(\cos\phi+\phi\sin\phi)\\ y=a(\sin\phi-\phi\cos\phi)\end{array}\right.$

This is a curve described by the endpoint $P$ of a string as it unwinds from a circle of radius $a$ while held taut.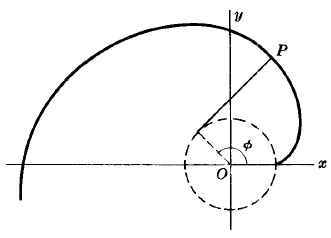

EVOLUTE OF AN ELLIPSE
Equation in ractangular coordinates:
$(ax)^\frac{2}{3}+(by)^\frac{2}{3}=(a^2-b^2)^\frac{2}{3}$

Parametric equations:
$\left\{\begin{array}{lr}ax=(a^2-b^2)\cos^3\theta\\ by=(a^2-b^2)\sin^3\theta\end{array}\right.$
This curve is the envelope of the normals to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.

OVALS OF CASSINI
Polar equation: $r^4+a^4-2a^2r^2\cos2\theta=b^4$.

This is the curve described by point $P$ such that the product of its distances from two fixed points[distance $2a$ apart] is a constant $b^2$.

The curve is as in the figures according as $b < a$ or $b > a$ respectively.

If $b = a$, the curve is a lemniscate

LIMASCON OF PASCAL
Polar equation: $r = b + a\cos\theta$

Let $OQ$ be a line joining origin $O$ to any point $Q$ on a circle of diameter $a$ passing through $O$.Then the curve is the locus of all points $P$ such that $PQ = b$.

The curve is as in the figures below according as $b > a$ or $b < a$ respectively. If $b = a$, the curve is a cardioid.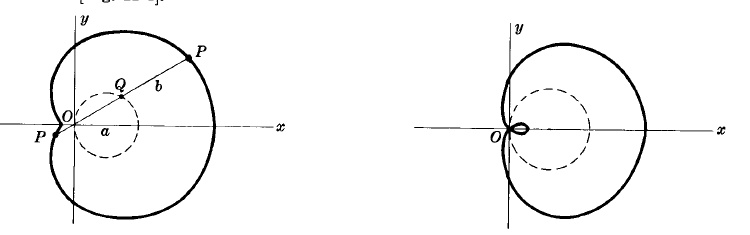

CISSOID OF DIOCLES
Equation in rectangular coordinates: $y^2=\frac{x^3}{2a - x}$

Parametric equations:
$\left\{\begin{array}{lr}x=2a\sin^2\theta\\ y=\frac{2a\sin^3\theta}{\cos\theta}\end{array}\right.$

This is the curve described by a point $P$ such that the distance $OP =$ distance $RS$. It is used in the problem if duplication of a cube, i.e. finding the side of a cube which has twice the volume of a given cube.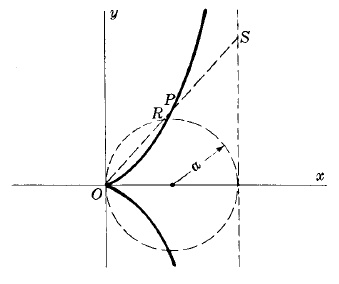

SPIRAL OF ARCHIMEDES
Polar equation: $r = a\theta$