Domain and Range
Author: Sepehr HassannejadPart 2
Definition:
The set of first components of pairs of elements of $f$ is called domain and the the set of second component is called range. Domain and range of a function denoted by $D_f$ and $R_f$ respectively.
Talking mathematically
$D_f=\lbrace x |(x,y) \in f \rbrace$
$R_f= \lbrace y | (x,y) \in f \rbrace $
$R_f= \lbrace y | (x,y) \in f \rbrace $
Example:
Let $f=\lbrace (1,-1),(3,3),(7,-1),(5,3) \rbrace$. Determine $D_f$ and $R_f$.
Solution:
$D_f=\lbrace 1,3,5,7 \rbrace$
$R_f= \lbrace -1,3 \rbrace$
$R_f= \lbrace -1,3 \rbrace$
Example:
If $D_f=R_f=\lbrace 1,2,3 \rbrace$, then how many different functions can be made with the domain and range?
Solution:
$f=\lbrace (1, \bigcirc ),(2 , \bigcirc),(3,\bigcirc) \rbrace$
The first position can be filled with 1 or 2 or 3, therefore there are three different ways to fill the first one. The second and the third position can be filled with three
different ways, too. So there are $ 3 \times 3 \times 3=27$ ways totally. It means that 27 different functions can be made with the $D_f$ and $R_f$. Some of them are written below. It also can be proven, giving all possible solutions.
$f_1 = \lbrace (1,1),(2,2),(3,3) \rbrace$
$f_2 = \lbrace (1,1),(2,1),(3,1) \rbrace$
$f_3 = \lbrace (1,1),(2,3),(3,2) \rbrace$
$f_2 = \lbrace (1,1),(2,1),(3,1) \rbrace$
$f_3 = \lbrace (1,1),(2,3),(3,2) \rbrace$
Practical methods for finding domain and range of real functions
If $f$ is defined with set of pairs or a table, then domain and rage are clearly determined.Example:
Determine domain and range of $f=\lbrace (1,4),(2,5),(3,6) \rbrace$.
Solution:
$D_f=\lbrace 1,2,3 \rbrace \,\,,\,\, R_f= \lbrace 4,5,6 \rbrace$
Mathematically
$D_f= \lbrace x | x \in \mathbb{N} , 1 \leq x \leq 3 \rbrace$
$R_f= \lbrace x | x \in \mathbb{N} , 4 \leq x \leq 6 \rbrace$
Example:
Determine domain and range of
$f=\lbrace (1,1),(2,3),(3,5),(4,7),(5,9),(6,11),(7,1),(8,7),(9,8),(10,9),(11,10) \rbrace$.
Then define the function.
Solution:
$D_f=\lbrace 1,2,3 , \cdots ,11 \rbrace = \lbrace x| x \in \mathbb{N} , x \leq 11 \rbrace$
$R_f= \lbrace 1,3,5,7,8,9,10,11 \rbrace$
$f(x)=
\begin{cases}
2x-1 \,\,\,\,\,\,\,\,\,\,\,\, x \leq 6 \,\,\,\, x \in \mathbb{N}\\
1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=7\\
x-1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, 1 \leq x \leq 8 \,\,\,\, x \in \mathbb{N}
\end{cases}$
Example:
Determine domain and range of the below piecewise function. Then try to define it with sets of pairs and finally sketch the graph of it.
$f(x)=
\begin{cases}
1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0\\
0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=0\\
-1 \,\,\,\,\,\,\,\,\,\,\,\, x<0
\end{cases}$
Solution:
It is obvious that
$D_f= \mathbb{R} \,\,,\,\, R_f= \lbrace -1,0,1 \rbrace $
$f(x)=f_1 \cup f_2 \cup f_3=
\begin{cases}
f_1 = \lbrace (x,y) | x \in \mathbb{R^+} \,\,,\,\, y=1 \rbrace \\
f_2 = \lbrace (0,0) \rbrace \\
f_3 = \lbrace (x,y) | x \in \mathbb{R^-} \,\,,\,\, y=-1 \rbrace
\end{cases}$

Tip:
This function is also called sign function and is denoted by $\textit{Sgn(x)}$.
$Sgn(x)=
\begin{cases}
1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0 \\
0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=0 \\
-1 \,\,\,\,\,\,\,\,\,\,\,\, x<0
\end{cases}$
Exercises
Determine the domain and range of the functions.
1) $f(x)= \begin{cases} 3 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>1 \\ 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=1 \\ -3 \,\,\,\,\,\,\,\,\,\,\,\, x<1 \end{cases}$
2) $g(x)= \begin{cases} -1 \,\,\,\,\,\,\,\,\,\,\, x<0 \\ 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0 \end{cases} $
3) $h(x)= \begin{cases} -2 \,\,\,\,\,\,\,\,\,\,\,\,-2 < x \leq 2 \\ \sqrt{2} \,\,\,\,\,\,\,\,\,\,\,\, x=5 \\ -3 \,\,\,\,\,\,\,\,\,\,\,\, x>4 \end{cases} $
4)$k(x)= \begin{cases} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x\geq 2 \\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x < 0 \end{cases}$
Polynomial function
Definition:$f$ is called polynomial function if and only if for every real valued $x$ ($x \in \mathbb{R}$)
$f(x)=a_n x^n+a_{n-1} x^{x-1}+\cdots+a_1 x+a_0 \,\,\,\,\,\,\,\, n \in \mathbb{N} \cup \lbrace 0 \rbrace$
Real valued $a_0,a_1,\cdots,a_n$ are called coefficient of polynomial and the non-negative integer $n$ if $a_n \neq 0$ is called degree of polynomial.
Domain of a polynomial function is $\mathbb{R}$. For determining range of a polynomial function first the equation should be solved in terms of $y$, which means $x$ should be in one side of the equation and constant numbers and $y$ should be the other side. Then it is easy to find the range of function by using some rules.
Tip:
In most cases if $ n \geq 5$, then it is not easy to find the range of a polynomial function.
Example:
Determine domain and range of $f(x)=x^2+1$.
Solution:
It is clear that $D_f=\mathbb{R}$. On the other hand
$y=x^2+1 \rightarrow y-1=x^2 \geq 0 \rightarrow y-1 \geq 0 \rightarrow y \geq 1 \rightarrow R_f=[1,+\infty)$
Also the graph of the function is

Example:
Determine domain and range of $f(x)=-x^2+1$.
Solution:
It is clear that $D_f=\mathbb{R}$. Also notice that
$y=-x^2+1 \rightarrow x^2=1-y \rightarrow x=\pm \sqrt{1-y} \rightarrow 1-y \geq 0 \rightarrow y \leq 1 \rightarrow
$
$
$R_f=(-\infty,1]$
Also the graph of the function is

Example:
Determine domain and range of $f(x)=x^4-2x^2+4$.
Solution:
As I've already said $D_f=\mathbb{R}$
$y=x^4-2x^2+4 \rightarrow x^4-2x^2+4-y=0 \\ \rightarrow x^2= \dfrac{2 \pm \sqrt{4-4(4-y)}}{2}=1 \pm \sqrt{1-(4-y)} \rightarrow x=\pm \sqrt{1 \pm \sqrt{y-3}}$
Notice that
$\begin{cases}
y-3 \geq 0 \rightarrow 3 \leq y \rightarrow R_1=[-3,\infty) \\
1-\sqrt{y-3} \geq 0 \rightarrow \sqrt{y-3} \leq 1 \rightarrow 0 \leq y-3 \leq 1 \rightarrow 3 \leq y \leq 4 \rightarrow R_2=[3,4]
\end{cases}$
Therefore
$R_f=R_1 \cup R_2=[3,+\infty)$
Also the graph of the function is

Exercises
Determine the domain and range of the functions.1)$y=-x^2+2$
2)$y=x^2+6x+1$
3)$y=x^3+6x^2+3x+1$
4)$y=-x^4+2x^2+1$
5)$y=x^5-5x+1$
6)$y=x^{10}+10x+2$
7)$y=x^{100}-100x+99$
8)$y=x^{101}+7x+4$
Fractional function
Definition:A fractional function which in its denominator and numerator are polynomial is called rational function.
Domain of a fractional function is all the real numbers except the roots of denominator of the fraction.
General form of a fractional function is
$f(x)=\dfrac{a_nx^n+\cdots+a_1x+a_0}{b_nx^n+\cdots+b_1x+b_0}=\dfrac{P(x)}{Q(x)}$
$D_f=\mathbb{R} - \lbrace x| Q(x)=0 \rbrace$
Example:
Determine domain and range of $f(x)=\dfrac{x^2+1}{x^2-1}$.
Solution:
First the roots of the denominator should be found.
$x^2-1=0 \rightarrow x=\pm 1$
Therefore domain of the function is
$D_f=\mathbb{R}- \lbrace \pm 1 \rbrace$
On the other hand
$y(x^2-1)=x^2+1 \rightarrow yx^2-x^2=y+1 \rightarrow x^2=\dfrac{y+1}{y-1} \\ \rightarrow x= \pm \sqrt{\dfrac{y+1}{y-1}} \rightarrow \dfrac{y+1}{y-1} \geq 0 \\ \rightarrow y \leq -1 \,\, or \,\, y > 1 \rightarrow R_f=(-\infty,-1] \cup (1,+\infty).$
Here is the graph of $f$

Example:
Determine domain and range of $y=\dfrac{x^2+3x-4}{x^2-2x+1}$.
Solution:
$x^2-2x+1=0 \rightarrow (x-1)^2=0 \rightarrow x=1 \rightarrow D_f=\mathbb{R}-\lbrace 1 \rbrace$
On the other hand
$y=\dfrac{x^2+3x-4}{(x-1)^2}=\dfrac{x+4}{x-1} \rightarrow xy-y=x+4 \rightarrow x=\dfrac{y+4}{y-1} \rightarrow R_f=\mathbb{R}- \lbrace 1 \rbrace$
Also graph of the function is

Example:
Determine domain and range of $f(x)=\dfrac{x^3+3x^2+2x}{x(x+1)(x^2-4)}$
Solution:
The roots of the denominator are
$x(x+1)(x^2-4)=0 \rightarrow x=0 \,\,,\,\, x=-1 \,\,,\,\, x= \pm 2 \rightarrow D_f=\mathbb{R}-\lbrace 0,-1 , \pm 2 \rbrace$
After simplifying the function, it would be
$f(x)=\dfrac{1}{x-2}$
On the other hand for defining the range of $f$, the value of the function at each points $x=0\,\,,\,\,x=-1 \,\,,\,\, x=-2$ should be determined.
$f(0)=-\dfrac{1}{2} \,\,,\,\, f(-1)=-\dfrac{1}{3} \,\,,\,\, f(-2)=-\dfrac{1}{4}$
Also notice
$y=\dfrac{1}{x-2} \rightarrow x=\dfrac{1}{y}+2$
Therefore
$R_f=\mathbb{R}-\lbrace -\dfrac{1}{2},-\dfrac{1}{3},-\dfrac{1}{4},0 \rbrace$
Here is the graph of $f$

Exercises
1) $y=\dfrac{2x+2}{x-1}$
2) $y=\dfrac{x^3+x}{x}$
3) $y=\dfrac{x^2-2x}{x^2+3x}$
4) $y=\dfrac{x^{100}-x}{x-x^{100}}$
5) $y=\dfrac{-2}{x^2+x+1}$
6) $y=\dfrac{-x^2-3}{x^2+4}$
7) $y=\dfrac{x^7-x^6}{x^7+x^6}$
8) $y=\dfrac{x^3-x}{x^3+x}+\dfrac{1-x}{x-1}+\dfrac{x^2-4}{4-x^2}$
9) $y=\dfrac{x^3-3x+2}{x^2+x-2}$
10) $y=\dfrac{1}{x^3+1}$
11) $y=\dfrac{x^{10}+x^8}{x^6+x^4}$
Irrational function
If $x$ in a function is under radical, then the function is called irrational function. General form of this kind of function is
$f(x)=\sqrt[n]{P(x)}$
If $P(x)$ is a polynomial and $n$ is an odd number, then the domain of $f$ is all the real numbers $\,\, \mathbb{R}$. On the other hand if $n$ is an even number, then the domain of $f$ is the set of all numbers which make the statement under the radical be non-negative.
Notice that radical of a negative number is not defined in real numbers.
Example:
Determine domain and range of $f(x)=\sqrt{\dfrac{x^2-3x}{-x^2+2x+3}}$.
Solution:
$D_f=\lbrace x \in \mathbb{R} | \dfrac{x^2-3x}{-x^2+2x+3} \geq 0 \rbrace$
So
$\dfrac{x^2-3x}{-x^2+2x+3} \geq 0 \rightarrow \dfrac{x^2-3x}{-x^2+2x+3}=0 \rightarrow x=0 \,\,,\,\, x=-1 \,\,,\,\, x=3$

$ D_f = (-1,0]$
On the other hand
$y=\sqrt{\dfrac{x(x-3)}{-(x+1)(x-3)}} \geq 0$
Also
$y=\sqrt{\dfrac{x}{-(x+1)}} \rightarrow y^2=\dfrac{x}{-(x+1)} \rightarrow x=\dfrac{-y^2}{1+y^2} \in (-1,0] \rightarrow $
$-1<\dfrac{-y^2}{1+y^2} \leq 0 \rightarrow 0<\dfrac{1}{1+y^2} \leq 1 \rightarrow y^2 \geq 0 \rightarrow y \in \mathbb{R} \rightarrow$
$ \mathbb{R} \cap [0,+\infty)=[0,+\infty) \rightarrow R_f=[0,+\infty)$
Here is the graph of $f$
Tip:
If $a>0$, then $a+\dfrac{1}{a}\geq 2$
Example:
Determine domain and range of $f(x)=\dfrac{x^4+2}{\sqrt{x^4+1}}$.
Solution:
Notice
$x^4+1>0 \rightarrow D_f=\mathbb{R}$
Also for defining range
$y=\dfrac{x^4+1+1}{\sqrt{x^4+1}}=\sqrt{x^4+1}+\dfrac{1}{\sqrt{x^4+1}}$
According to the inequality mentioned
$y=\sqrt{x^4+1}+\dfrac{1}{\sqrt{x^4+1}}\geq 2 \rightarrow R_f=[2,+\infty)$
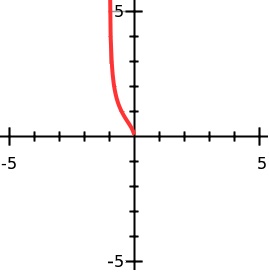
Here is the graph of $f$

Exercises
Determine domain and range.1) $f(x)=\sqrt{x^2-4x+5}$
2) $f(x)=\dfrac{\sqrt[8]{2x-2\sqrt{x}}}{\sqrt[6]{4-x^2}}+\dfrac{\sqrt[4]{1+x^2}}{\sqrt{2x-x^2}}$
3) $f(x)=\sqrt{x-1}$
4) $f(x)=\sqrt{\dfrac{1-x}{x+1}}$
5) $f(x)=\sqrt{\dfrac{x^3}{x^4+x^3}}$
6) $f(x)=\sqrt{4-x^2}$
7) $f(x)=\sqrt{\dfrac{x^3-1}{x-1}}$
8) $f(x)= \sqrt[4]{\dfrac{x^3-3x+2}{x^2-2x+1}}$
9) $f(x) =\dfrac{\sqrt{x}}{\sqrt{x-1}}$
10) $f(x)=\sqrt{\dfrac{x-x^2}{x}}$
11) $f(x)=\sqrt{\dfrac{x^2-2x}{x-2}}+\sqrt{\dfrac{x^2-4x}{x-4}}$
12) $f(x)=\dfrac{\sqrt{x-1}}{\sqrt{x^2-x}}$
Integral part function
Definition:Floor function maps a real number to the largest previous integer. More precisely, $\lfloor x \rfloor$ is the largest integer not greater than $x$.
Graph of floor function is

Definition:
The fractional part, denoted by $\lbrace x \rbrace$ for real $x$, is defined by the formula
$\lbrace x \rbrace = x - \lfloor x \rfloor$
It is clear that
$ 0 \leq \lbrace x \rbrace <1$
Properties:1) $ \lfloor x \rfloor = max \lbrace a \in \mathbb{Z} | a \leq x \rbrace$
2) $ \lfloor x \rfloor \leq x \leq \lfloor x \rfloor +1$
3) $x-1 \leq \lfloor x \rfloor \leq x$
4) $\lfloor x-\lfloor x \rfloor \rfloor =0$
5) $\lfloor x+a \rfloor = \lfloor x \rfloor +a \,\,\,\, a \in \mathbb{Z}$
6) $ \lfloor x \rfloor + \lfloor y \rfloor \leq \lfloor x+y \rfloor \leq \lfloor x \rfloor + \lfloor y \rfloor +1$
7) $\lfloor x \rfloor + \lfloor -x \rfloor=$ $\begin{cases} 0 \,\,\,\,\,\, x \in \mathbb{Z} \\ -1 \,\,\,\, x \in \mathbb{R}-\mathbb{Z} \end{cases}$
8)$\lfloor \lfloor x \rfloor \rfloor=\lfloor x \rfloor$
9) $\lfloor \dfrac{x+m}{n} \rfloor= \lfloor \dfrac{\lfloor x \rfloor+m}{n} \rfloor \,\,\,\, m,n \in \mathbb{Z} \,\,,\,\, n>0 $
10)$\lfloor n \rfloor =\lfloor \dfrac{n}{m} \rfloor + \lfloor \dfrac{n+1}{m} \rfloor \cdots + \lfloor \dfrac{n+m-1}{m} \rfloor \,\,\,\, m,n \in \mathbb{Z} \,\,,\,\, m>0$
11) $\lfloor mx \rfloor = \lfloor x \rfloor + \lfloor x+\dfrac{1}{m} \rfloor + \cdots + \lfloor x+\dfrac{m-1}{m} \rfloor \,\,\,\, m \in \mathbb{Z} \,\,,\,\, m>0$
12) $ \lfloor \dfrac{\lfloor \dfrac{x}{m} \rfloor}{n} \rfloor = \lfloor \dfrac{x}{mn} \rfloor \,\,\,\, m,n \in \mathbb{N}$
For finding domain and range of a floor function, one should use the above properties.
Example:
Determine domain and range of $f(x)=\dfrac{x-\lfloor x-\lfloor x \rfloor \rfloor}{x+\lfloor x \rfloor+\lfloor -x \rfloor}$.
Solution:
According to the properties
$\lfloor x-\lfloor x \rfloor \rfloor =0$
and
$ \lfloor x \rfloor + \lfloor -x \rfloor =
\begin{cases}
0 \,\,\,\,\,\,\,\,\,\,\, x \in \mathbb{Z} \\ \\
-1 \,\,\,\,\,\,\, x \in \mathbb{R}-\mathbb{Z}
\end{cases}$
So
$y=
\begin{cases}
\dfrac{x}{x}=1 \,\,\,\, x \in \mathbb{Z} - \lbrace 0 \rbrace
\\
\\
\dfrac{x}{x-1} \,\,\,\,\, x \in \mathbb{R}-\mathbb{Z}
\end{cases}$
Therefore
$D_f=\mathbb{R}-\lbrace 0 \rbrace$
Also for range
$x \in \mathbb{R}-\mathbb{Z}: y=\dfrac{x}{x-1} \rightarrow x =\dfrac{y}{y-1} \in \mathbb{R} - \mathbb{Z} \rightarrow y =\neq 1$
$R_f=\mathbb{R}- \lbrace \dfrac{k}{k-1} | k \in \mathbb{Z}- \lbrace 1 \rbrace \rbrace $
Example:
Determine domain and range $f(x)=\dfrac{\lfloor x+1 \rfloor+\lfloor -x \rfloor}{\lfloor 1-x \rfloor+\lfloor x \rfloor}$
Solution:
$f(x)=\dfrac{\lfloor x+1 \rfloor+\lfloor -x \rfloor}{\lfloor 1-x \rfloor+\lfloor x \rfloor}=\dfrac{\lfloor x \rfloor+\lfloor -x \rfloor+1}{\lfloor -x \rfloor+\lfloor x \rfloor+1}=
\begin{cases}
1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x \in \mathbb{Z}
\\
Undefined \,\,\,\,\,\,\,\, x \in \mathbb{R}-\mathbb{Z}
\end{cases}$
Therefore
$D_f=\mathbb{Z} \,\,\,\,,\,\,\,\, R_f=\lbrace 1 \rbrace$
Graph of $f$ is

Exercises
Determine domain and range.1) $f(x)=\dfrac{2x+1}{\lfloor 1-x \rfloor+\lfloor x+1 \rfloor}+\dfrac{\lfloor \lfloor x \rfloor -x \rfloor}{\lfloor x \rfloor + \lfloor -x \rfloor}$
2) $f(x)=\lfloor \dfrac{x^4+2x^2+2}{x^4+4x^2+5} \rfloor + \dfrac{x-\lfloor x \rfloor}{\lfloor x+1 \rfloor + \lfloor 1-x \rfloor}$
3) $y=2\lfloor x \rfloor+2\lfloor -x \rfloor$
4) $y=\dfrac{\lfloor -x \rfloor+\lfloor x+2 \rfloor-2}{\lfloor x-2 \rfloor+\lfloor -x+2 \rfloor}$
5) $y=\dfrac{\lfloor \lfloor x \rfloor -x \rfloor}{\lfloor 1-x \rfloor+\lfloor x-1 \rfloor}$
6) $y=\dfrac{\lfloor 4-x \rfloor+\lfloor -x \rfloor}{\lfloor 3-x \rfloor+\lfloor 1-x \rfloor}$
7) $y=\dfrac{\lfloor -x \rfloor+\lfloor x+2 \rfloor}{\lfloor x+2 \rfloor+\lfloor -x \rfloor -2}$
8) $y=\dfrac{x}{\lfloor 1-x \rfloor+\lfloor x-1 \rfloor}$
9) $y=\dfrac{2\lfloor x \rfloor -2x}{x-\lfloor x \rfloor}$
10) $y=\dfrac{x-\lfloor x \rfloor}{\lfloor x \rfloor + \lfloor -x \rfloor}$
11) $y=\lfloor \dfrac{x^4+x^2+1}{x^4+x^2+2} \rfloor$
12) $y=(-1)^{\lfloor x-5 \rfloor+\lfloor 5-x \rfloor} $
Part 2

 MENU
MENU