Hyperbolic Functions - sinh, cosh, tanh, coth, sech, csch

Definition of hyperbolic functions

Hyperbolic sine of x
$\text{sinh}\ x = \frac{e^{x} - e^{-x}}{2}$

Hyperbolic cosine of x
$\text{cosh}\ x = \frac{e^x + e^{-x}}{2}$

Hyperbolic tangent of x
$\text{tanh}\ x = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

Hyperbolic cotangent of x
$\text{coth}\ x = \frac{e^x + e^{-x}}{e^x - e^{-x}}$

Hyperbolic secant of x
$\text{sech}\ x = \frac{2}{e^x + e^{-x}}$

Hyperbolic cosecant of x
$\text{csch}\ x = \frac{2}{e^x - e^{-x}}$

Relationship among hyperbolic functions

$\text{tanh}\ x = \frac{\text{sinh}\ x}{\text{cosh}\ x}$

$\text{coth}\ x = \frac{1}{\text{tanh}\ x} = \frac{\text{cosh}\ x}{\text{sinh}\ x}$

$\text{sech}\ x = \frac{1}{\text{cosh}\ x}$

$\text{csch}\ x = \frac{1}{\text{sinh}\ x}$

$\text{cosh}^2x - \text{sinh}^2x = 1$

$\text{sech}^2x + \text{tanh}^2x = 1$

$\text{coth}^2x - \text{csch}^2x = 1$

Functions of negative arguments

sinh(-x) = -sinh x

cosh(-x) = cosh x

tanh(-x) = -tanh x

csch(-x) = -csch x

sech(-x) = sech x

coth(-x) = -coth x

Addition fomulas

$\text{sinh}(x \pm y) = \text{sinh}\ x \ \text{cosh}\ y \pm \text{cosh}\ x\ \text{sinh}\ y$

$\text{cosh}(x \pm y) = \text{cosh}\ x\ \text{cosh}\ y \pm \text{sinh}\ x\ \text{sinh}\ y$

$\text{tanh}(x \pm y) = \frac{\text{tanh}\ x \pm \text{tanh}\ y}{1 \pm \text{tanh}\ x \cdot \text{tanh}\ y}$

$\text{coth}(x \pm y) = \frac{\text{coth x}\ \text{coth}\ y \pm l}{\text{coth}\ y \pm \text{coth}\ x}$

Double angle formulas

$\text{sinh}\ 2x = 2 \text{sinh}\ x\ \text{cosh}\ x$

$\text{cosh}\ 2x = \text{cosh}^2x + \text{sinh}^2x= 2 \text{cosh}^2x - 1 = 1 + 2 \text{sinh}^2x$

$\text{tanh}\ 2x = \frac{2\text{tanh}\ x}{1 + \text{tanh}^2x}$

Half angle formulas

$\sinh \frac{x}{2} = \pm \sqrt{\frac{\cosh x - 1}{2}}$ [+ if x > 0, - if x < 0]

$\cosh \frac{x}{2} = \sqrt{\frac{\cosh x + 1}{2}}$

$\tanh \frac{x}{2} = \pm \sqrt{\frac{\cosh x - 1}{\cosh x + 1}}$ [+ if x > 0, - if x < 0]

$=\frac{\text{sinh}(x)}{1 + \text{cosh}(x)} = \frac{\text{cosh}(x) - 1}{\text{sinh}(x)}$

Multiple angle formulas

$\sinh 3x = 3 \sinh x + 4 \sinh^3 x$

$\cosh 3x = 4 \cosh^3 x - 3 \cosh x$

$\tanh 3x = \frac{3 \tanh x + \tanh^3 x}{1 + 3 \tanh^2x}$

$\sinh 4x = 8 \sinh^3 x\ \cosh x + 4 \sinh x\ \cosh x$

$\cosh 4x = 8 \cosh^4 x - 8 \cosh^2 x + 1$

$\tanh 4x = \frac{4 \tanh x + 4 \tanh^3 x}{1 + 6 \tanh^2 x + \tanh^4 x}$

Powers of hyperbolic functions

$\text{sinh}^2 x = \frac12 \text{cosh}\ 2x - \frac12$

$\text{cosh}^2 x = \frac12 \text{cosh}\ 2x + \frac12$

$\text{sinh}^3 x = \frac14 \text{sinh}\ 3x - \frac34 \text{sinh}\ x$

$\text{cosh}^3 x = \frac14 \text{cosh}\ 3x + \frac34 \text{cosh}\ x$

$\text{sinh}^4 x = \frac{3}{8} - \frac12 \text{cosh}\ 2x + \frac18 \text{cosh}\ 4x$

$\text{cosh}^4 x = \frac{3}{8} + \frac12 \text{cosh}\ 2x + \frac18 \text{cosh}\ 4x$

Sum, difference and product

$\text{sinh}\ x + \text{sinh}\ y = 2 \text{sinh}\ \frac12(x + y)\ \text{cosh}\ \frac12(x - y)$

$\text{sinh}\ x - \text{sinh}\ y = 2 \text{cosh}\ \frac12(x + y)\ \text{sinh} \frac12(x - y)$

$\text{cosh}\ x + \text{cosh}\ y = 2 \text{cosh}\ \frac12(x + y)\ \text{cosh}\ \frac12(x - y)$

$\text{cosh}\ x - \text{cosh}\ y = 2 \text{sinh}\ \frac12(x + y)\ \text{sinh}\ \frac12(x - y)$

$\text{sinh}\ x\ \text{sinh}\ y = \frac12(\text{cosh}(x + y) - \text{cosh} (x - y))$

$\text{cosh}\ x\ \text{cosh}\ y = \frac12(\text{cosh}(x + y) + \text{cosh} (x - y))$

$\text{sinh}\ x\ \text{cosh}\ y = \frac12(\text{sinh}(x + y) + \text{sinh} (x - y))$

Expression of hyperbolic functions in terms of others

In the following we assume x > 0. If x < 0 use the appropriate sign as indicated by formulas in the section "Functions of Negative Arguments"

~	$\text{sinh}\ x = u$	$\text{cosh}\ x = u$	$\text{tanh}\ x = u$	$\text{coth}\ x = u$	$\text{sech}\ x = u$	$\text{csch}\ x = u$
$\text{sinh}\ x$	$u$	$\sqrt{u^2 - 1}$	$\frac{u}{\sqrt{1 - u^2}}$	$\frac{1}{\sqrt{u^2 - 1}}$	$\frac{\sqrt{1 - u^2}}{u}$	$\frac{1}{u}$
$\text{cosh}\ x$	$\sqrt{1 + u^2}$	$u$	$\frac{1}{\sqrt{1 - u^2}}$	$\frac{u}{\sqrt{u^2 - 1}}$	$\frac{1}{u}$	$\frac{\sqrt{1 + u^2}}{u}$
$\text{tanh}\ x$	$\frac{u}{\sqrt{1 + u^2}}$	$\frac{\sqrt{u^2 - 1}}{u}$	$u$	$\frac{1}{u}$	$\sqrt{1 - u^2}$	$\frac{1}{\sqrt{1 + u^2}}$
$\text{coth}\ x$	$\frac{\sqrt{1 + u^2}}{u}$	$\frac{u}{\sqrt{u^2 - 1}}$	$\frac{1}{u}$	$u$	$\frac{1}{\sqrt{1 - u^2}}$	$\sqrt{1 + u^2}$
$\text{sech}\ x$	$\frac{1}{\sqrt{1 + u^2}}$	$\frac{1}{u}$	$\sqrt{1 - u^2}$	$\frac{\sqrt{u^2 - 1}}{u}$	$u$	$\frac{u}{\sqrt{1 + u^2}}$
$\text{csch}\ x$	$\frac{1}{u}$	$\frac{1}{\sqrt{u^2 - 1}}$	$\frac{\sqrt{1 - u^2}}{u}$	$\sqrt{u^2 - 1}$	$\frac{u}{\sqrt{1 - u^2}}$	$u$

Graphs of hyperbolic functions

y = sinh x

y = cosh x

y = tanh x

y = coth x

y = sech x

y = csch x

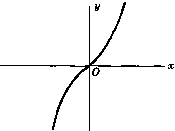
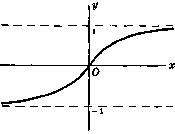
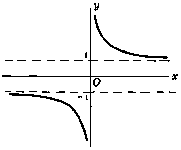
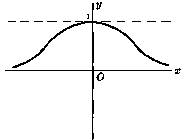
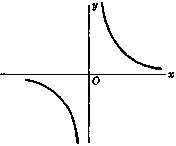
Inverse hyperbolic functions

If x = sinh y, then y = sinh^-1 a is called the inverse hyperbolic sine of x. Similarly we define the other inverse hyperbolic functions. The inverse hyperbolic functions are multiple-valued and as in the case of inverse trigonometric functions we restrict ourselves to principal values for which they can be considered as single-valued.

The following list shows the principal values [unless otherwise indicated] of the inverse hyperbolic functions expressed in terms of logarithmic functions which are taken as real valued.

$\sinh^{-1} x = \ln(x + \sqrt{x^2 + 1})$ $-\infty < x < \infty$

$\cosh^{-1} x = \ln(x + \sqrt{x^2 - 1})$ $x \geq l$ [$\cosh^{-1} x > 0$ is principal value]

$\tanh^{-1} x = \frac{1}{2} \ln\frac{(1 + x)}{(1 - x)}$ $- 1 < x < 1$

$\coth^{-1} x = \frac{1}{2} \ln\frac{(x + 1)}{(x - 1)}$ $x > 1$ or $x < -1$

$\text{sech}^{-1} x = \ln(\frac{1}{x} + \sqrt{\frac{1}{x^2} - 1})$ $0 < x \leq l$ [$\text{sech}^{-1} x > 0$ is principal value]

$\text{csch}^{-1} x = \ln(\frac{1}{x} + \sqrt{\frac{1}{x^2} + 1})$ $x \neq 0$

Relationship between inverse hyperbolic functions

csch^-1 x = sinh^-1 (1/x)

sech^-1 x = cosh^-1 (1/x)

coth^-1 x = tanh^-1 (1/x)

sinh^-1(-x) = -sinh^-1x

tanh^-1(-x )= -tanh^-1x

coth^-1 (-x) = -coth^-1x

csch^-1 (-x) = -csch^-1x

Graphs of inverse hyperbolic functions

y = sinh^-1x

y = cosh^-1x

y = tanh^-1x

y = coth^-1x

y = sech^-1x

y = csch^-1x

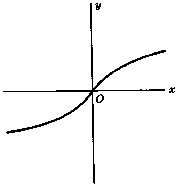
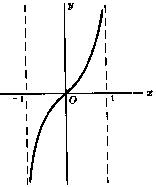
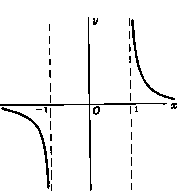
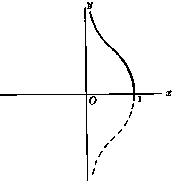
Relationship between hyperbolic and trigonometric functions

$\sin(ix) = i \text{sinh}\ x$	$\cos(ix) = \text{cosh}\ x$	$\tan(ix) = i \text{tanh}\ x$
$\csc(ix) = -i \text{csch}\ x$	$\sec(ix) = \text{sech}\ x$	$\cot(ix) = -i \text{coth}\ x$
$\text{sinh}(ix) = i \sin x$	$\text{cosh}(ix) = \cos x$	$\text{tanh}(ix) = i \tan x$
$\text{csch}(ix) = -i \csc x$	$\text{sech}(ix) = \sec x$	$\text{coth}(ix) = -i \cot x$

Periodicity of hyperbolic functions

In the following $k$ is any integer.

$\text{sinh} (x + 2k \pi i) = \text{sinh}\ x$ $\text{csch} (x + 2k\pi i) = \text{csch} x$

$\text{cosh} (x + 2k \pi i) = \text{cosh}\ x$ $\text{sech} (x + 2k\pi i) = \text{sech} x$

$\text{tanh} (x + k\pi i) = \text{tanh}\ x$ $\text{coth} (x + k\pi i) =\text{coth} x$

Relationship between inverse hyperbolic and inverse trigonometric functions

sin^-1 (ix) = isinh^-1x	sinh^-1(ix) = i sin^-1x
cos^-1 x = ±i cosh^-1 x	cosh^-1x = ±i cos^-1x
tan^-1(ix) = i tanh^-1x	tanh^-1(ix) = i tan^-1x
cot^-1(ix) = -i coth^-1x	coth^-1 (ix) = -i cot^-1x
sec^-1 x = ±i sech^-1x	sech^-1 x = ±i sec^-1x
csc^-1(ix) = -i csch^-1x	csch^-1(ix) = -i csc^-1x