Absolute Values
In this lecture we shall discuss:
- Absolute values
- Inequalities involving absolute values
- Theorem 1.2.2 (√a2=|a|)
- Theorem inequality
1.2.1 Definition
The absolute value or magnitude of a real number a is denoted by |a| and is defined by
Example
|5|=5 Since 5>0
|-4/7|= -(-4/7) = 4/7 Since -4/7<0
|0|=0 Since 0≥0
Remark
|a| is a non-negative number for all values of a and
-|a|≤ a ≤ |a|
If a itself is negative, then -a is positive and +a is negative!!!
Example
Solve |x-3|=4
Solution
| x-3= 4 x= 7 |
or | -(x-3)= 4 x-3= -4 x= -1 |
Example
Solve |3x-2|=|5x+4|
| 3x-2 = 5x+4 3x-5x = 4+2 -2x = 6 x = -3 |
or | 3x-2 = -(5x+4) . . x = $-\frac{1}{4}$ |
SQUARE ROOTS AND ABSOLUTE VALUES
b2 = a
(3)2 = 9
so b = 3
but!!!
(-3)2 = 9 so b = -3
The positive square root of the square of a number is equal to that number.
THEOREM 1.2.2
For any real number a
√a2 = |a|
e.g.
√(-4)2 = √16 = 4 = |-4|
1.2.3 THEOREM
If a and b are real numbers then,
- |-a| = |a| a number and its negative have the same absolute values.
- |ab| = |a||b| The absolute value of a product is the product of the absolute values.
- |a/b| = |a|/|b| The absolute value of a ratio is the ratio of the absolute values.
Proof
From theorem 1.2.2
(a) |-a| = √(-a)2 = √a2 = |a|
(b) |ab| = √(ab)2 = √a2b2 = √a2√b2 = |a||b|
Examples
(a) |-4| = |4|
(b) |2.-3| = |-6| = 6 = |2|.|3| = 6
(c) |5/4| = 5/4 = |5|/|4| = 5/4
The result (b) of above theorem can be extended to three or more factors.
For n-many real numbers
a1, a2, a3,...an
(a) |a1 a2 ...an| = |a1| |a2| ...|an|
(b) |an| = |a|n
Geometric interpretation of Absolute Value

Where A and B are points with coordinate a and b. The distance between A and B is

Theorem 1.2.4 (Distance formula)
If A and B are points on a coordinate line with coordinates a and b respectively, then the distance d between A and B
d = |b - a|
TABLE 1.2.2 (a)
|x-a| < k (k>0)
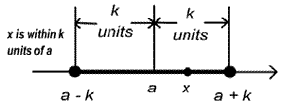
Alternative Form -k < x-a < k
Solution Set (a-k, a+k)
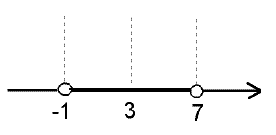
Example
The inequality
|x-3| < 4
rewritten as
-4 < x-3 < 4
adding 3 throughout gives
-1 < x < 7
solution set (-1,7)
On real line
Example
Solve |x+4| ≥ 2
| x+4 ≤ -2 x ≤ -6 |
x+4 ≥ 2 x≥ -2 |
(-∞ , -6] ∪ [-2 , +∞ )
On real line

THE TRIANGLE INEQUALITY
It is not generally true that
|a+b| = |a| + |b|
e.g.
if a = 2 and b = -3, then a+b = -1 so that |a+b| = |-1| = 1
whereas
|a|+|b| = |2|+|-3| = 2+3 = 5 so |a+b| = |a|+|b|
1.2.5 THEOREM - (Triangle Inequality)
If a b then |a+b| ≤ |a|+|b|
Proof
Since for any real number a and b, we know that
-|a| ≤ a ≤ |a| and -|b| ≤ b ≤ |b|
-|a| ≤ a ≤ |a|
+
-|b| ≤ b ≤ |b|
______________
= -|a| + -|b| ≤ a+b ≤ |a|+|b|
______________________________________________
Now we have two cases:
Case 1 where a+b ≥ 0
certainly a+b=|a+b|
Hence
|a+b| ≤ |a|+|b|
And
Case 2 where a+b < 0
|a+b| = -(a+b)
or
(a+b) = -|a+b|
Comparing with the intial inequality
-(|a|+|b|) ≤ -|a+b|
The result follows
←_______________________________→

 MENU
MENU