Logarithm(log, lg, ln)

If b = a^c <=> c = log_ab
a, b, c are real numbers and b > 0, a > 0, a ≠ 1
a is called "base" of the logarithm.
Example: 2³ = 8 => log₂8 = 3
the base is 2.

There are standrart notation of the logarithm if the base is 10 or e.

Graphs of logarithmic functions

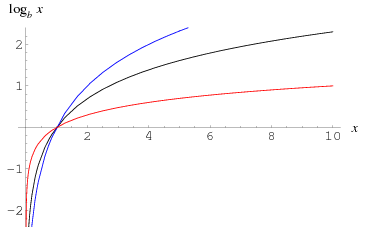
It shows that when x = 1, log = 0; when x -> 0 => log -> -∞; when x -> ∞ log -> ∞

Logarithm(log) properties

Logarithm calculator

If you have any question go to our forum about logarithms.