Limit and Continuity of Trigonometric Functions
Continuity of Sine and Cosine function

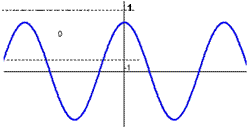
Here is the graph of Sinx and Cosx
-We consider angles in radians
-Insted of θ we will use x
f(x) = sin(x)

g(x) = cos(x)

It is evident that as h approaches 0, the coordinate of P approach the corresponding coordinate of B.

But by definition we know
sin(0) = 0 and cos(0) = 1
The values of the functions matche with those of the limits as x goes to 0 (Remind the definition of continuity we have).
limx → 0 sin(x) = sin(0) = 0 limx → 0 cos(x) = cos(0) = 1
Hence we have the following theorem
DEFINITION 2.7.1
A function f(x) is said to be continuous at a point c if the following conditions are sarisfied
-f(c) is defined
-limx → c f(x) exists
-limx → c f(x) = f(c)
THEOREM 2.8.1
The functions sin(x) and cos(x) are continuous
Proof
Let h = x - c. So x = h + c. Then x → c is equivalent to the requirement that h → 0
A function f(x) is continuous at c if the following conditions are true:
-f(c) is defined
-limh → 0 f(h + c) exists
-limh → 0 f(h + c) = f(c)
Assume
limx → 0 sin(x) = 0 and limx → 0 cos(x) = 1
The first two conditions of continuity definition are met. We have to show that
limh → 0 sin(c + h) = sin(c)
Now
limh → 0 sin(c + h) = limh → 0 [sin(c)cos(h) + cos(c)sin(h)] = limh → 0 sin(c)cos(h) + limh → 0 cos(c)sin(h) = sin(c)limh → 0 cos(h) + cos(c)limh → 0 sin(h) = sin(c)(1) + cos(c)(0) = sin(c)
Continuity of Other Trigonometric Functions
tan(x) = sin(x)/cos(x)
tan(x) is continuous everywhere except at cos(x) = 0 which gives
x = ± φ/2, ± 3φ/2, ± 5φ/2, ... = ± kφ/2 (k = 1, 3, 5, ...)
Similarly, since
cot(x) = cos(x)/sin(x)
sec(x) = 1/cos(x)
cosec(x) = 1/sin(x)
They are all continuous on appropriate ontervals using the continuity of sin(x) and cos(x).
Obtaining Limits by Squeezing
We will use Squeeze Theorem for finding limits
limx → 0 sin(x)/x = 1
limx → 0 [1 - cos(x)]/x = 0 Consider the graph of


Here the problem is:
- As x goes to 0, both thr top and the botton functions go to 0.
- sin(x) goes to 0 means that the fraction as a whole goes to 0.
- x goes to 0 means that the function as a whole goes to +∞.
Here we cannot write these functions in some other form by using algebraic Manipulation to solve this problem. So here we will use some other method. One such method is to obtain by following theorem:
Squeezing theorem
Let f, g and h be fucntions satisfying g(x)≤f(x)≤h(x) for all x in some open interval containg the point a, whit the possible exception that the inequalities need not hold at a.
If g and h have the same limits as x approaches a, say
limx → a g(x) = limx → a h(x) = L
then f also has this limit as x approaches a, that is
limx → a f(x) = L
Example:
Use the squeezing theorem to evaluate
limx → 0 x2sin2(1/x)
Solution
Remember that 0 ≤ sin(x) ≤ 1, so 0 ≤ sin2(x) ≤ 1 and so 0 ≤ sin2(1/x) ≤ 1
Multiply throughtout this last inequality by x2
0 ≤ x2sin2(1/x) ≤ x2
But limx → 0 0 = limx → 0 x2 = 0
So by the Squeezing Theorem
limx → 0 x2sin2(1/x) = 0
Before proving next theorem, let us see the following formula.
The proof will use basic facts about circles and areas of sectors with angle θ radians and raius r

The area of a sector is given by
A = (1/2).r2θ
THEOREM 2.8.3
limx → 0 sin(x)/x = 1
Let x be such that 0 < x < φ/2 or -φ/2 < x < 0
We made the assumption that
0 < x < φ/2
Also works when -φ/2 < x < 0

From the figure
0 < area of ΔOBP = (1/2) base.height = (1/2) (1).sin(x) = (1/2) sin(x)
area of sector OBP = (1/2)(1)2.x = (1/2)x
area of ΔOBQ = (1/2) base.height = (1/2) (1).tan(x) = (1/2)tan(x)
So, the above inequality becomes
0 < (1/2)sin(x) < (1/2)x < (1/2)tan(x)
Multiplying throughout by 2/sin(x)
1 < x/sin(x) < 1/cos(x)
Taking resiprocal gives
cos(x) < sin(x)/x < 1
Taking limit now and using Squeezing Theorem gives
limx → 0 cos(x) < limx → 0 sin(x)/x < limx → 0 1 = 1 < limx → 0 sin(x)/x < 1
Since the middles term is between 1 and 1, it must be 1

 MENU
MENU