The vertices, co-vertices and eccentricity of the ellipse $\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$ are:
Solution:
Answer: $V_{1}(-4,0),V_{2}(4,0);\ CV_{1}(0,-2),CV_{2}(0,2);e=\frac{\sqrt{3}}{2}$
$\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$
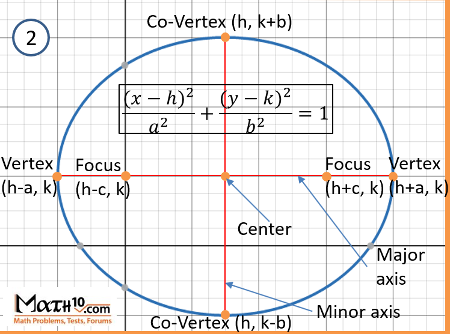
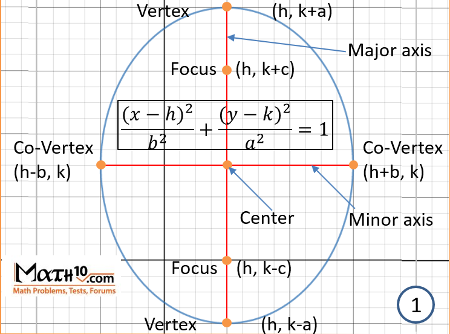
We know the equation $\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$ then
The vertices are at points $(h-a,k)\qquad (h+a,k)$ so
$V_{1}:(-4,0)\qquad V_{2}:(4,0)$
The co-vertices are at points $(h,k-b)\qquad (h,k+b)$ so
$CV_{1}:(0,-2)\qquad CV_{2}:(0,2)$
The eccentricity is $e=\frac{c}{a}=\frac{2\sqrt{3}}{4}\qquad e=\frac{\sqrt{3}}{2}$