Conic Sections: Problems with Solutions

Solution:
$2x^{2}+2y^{2}-4x-8y=40\Longrightarrow x^{2}+y^{2}-2x-4y=20$

$\left( x-1\right) ^{2}-1+\left( y-2\right)^{2}-4=20$

$\left( x-1\right) ^{2}+\left( y-2\right)^{2}=25$

is a circle with radius 5 and center $(1,2)$

Solution:
Answer: parabola.

$4x^{2}-4xy+y^{2}-6=0$

The general equation for any conic section is

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

A is 4.
B is -4.
C is 1.
The discriminant is $B^{2}-4AC=16-4(4)(1)=0\Longrightarrow $ is a parabola

Solution:
$2x^{2}-2xy+2y^{2}=1$

The general equation for any conic section is

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

A is 4.
B is -2.
C is 2.
The discriminant is
$B^{2}-4AC=4-4(2)(2)=-12<0$
The conic section is an ellipse.

Solution:
Answer: Hyperbola

$x^{2}-3xy+y^{2}=5$

The general equation for any conic section is

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

A is 1.
B is -3.
C is 1.
The discriminant is
$B^{2}-4AC=9-4(1)(1)=5>0\Longrightarrow $
This is a hyperbola.

Solution:
Answer: Hyperbola.

$4y^{2}-7x^{2}+1=-40y-42x$
$4y^{2}+40y-7x^{2}+42x+1=0$
$4(y^{2}+10y+25)-7(x^{2}-6x+9)-37+1=0$
$4(y+5)^{2}-7(x-3)^{2}=36$
$\frac{(y+5)^{2}}{9}-\frac{7(x-3)^{2}}{36}=1$ is a hyperbola

Solution:
Answer: Parabola.
$12x^{2}+72x+y=-109\Longrightarrow 12(x+3)^{2}-108+y=-109$

$\left( y+1\right) =-12(x+3)^{2}$
This is parabola.

Solution:
Answer: Circle.

$x^{2}+y^{2}+10x-6y+25=0\Longrightarrow (x+5)^{2}-25+(y-3)^{2}-9+25=0$

The equation $(x+5)^{2}+(y-3)^{2}=9$ is a circle
with radius 3 and center $(-5,3)$

Solution:
Answer: Ellipse.

We complete squares, then

$x^{2}+4y^{2}=4x-y\Longrightarrow x^{2}-4x+4y^{2}+y=0$

$\left( x-2\right)^{2}-4+4(y+\frac{1}{8})^{2}-\frac{1}{16}=0$ then

$\left( x-2\right)^{2}+4(y+\frac{1}{8})^{2}=4+\frac{1}{16}=\frac{65}{16}$ so

$\frac{\left( x-2\right) ^{2}}{\frac{65}{16}}+\frac{(y+\frac{1}{8})^{2}}{\frac{65}{64}}=1$
The equation represents an ellipse.

Solution:
Answer: Еllipse

$\cot 2\theta =\frac{A-C}{B}=\frac{1-1}{1}=0$ then $\theta =45^{\circ }$

$x=x' \cos \theta -y' \sin \theta =\frac{\sqrt{2}}{2}x' -\frac{\sqrt{2}}{2}y'$

$y=x' \sin \theta +y' \cos \theta =\frac{\sqrt{2}}{2}x' +\frac{\sqrt{2}}{2}y'$

$x^{2}+xy+y^{2}=4\Longrightarrow $
$\left( \frac{\sqrt{2}}{2}x' -\frac{\sqrt{2}}{2}y' \right) ^{2}+\left( \frac{\sqrt{2}}{2}x' -\frac{\sqrt{2}}{2}y' \right) \left( \frac{\sqrt{2}}{2}x' +\frac{\sqrt{2}}{2}y' \right) +\left( \frac{\sqrt{2}}{2}x' +\frac{\sqrt{2}}{2}y' \right) ^{2}=4$

$\frac{1}{2}\left( x' \right) ^{2}-x' y' +\frac{1}{2}\left( y' \right) ^{2}+\frac{1}{2}\left( x' \right) ^{2}-\frac{1}{2} \left( y' \right) ^{2}+\frac{1}{2}\left( x' \right) ^{2}+x' y' +\frac{1}{2}\left( y' \right) ^{2}=4$

$\frac{3}{2}\left( x' \right) ^{2}+\frac{1}{2}\left( y' \right) ^{2}=4\Longrightarrow \frac{3}{8}\left( x' \right) ^{2}+\frac{1}{8} \left( y' \right) ^{2}=1\Longrightarrow $

$\frac{\left( x' \right) ^{2}}{8/3}+\frac{\left( y' \right) ^{2}}{8}=1$ is an ellipse.

Solution:
Answer: Ellipse

$\cot 2\theta =\frac{5-1}{-3}=\frac{4}{3}>0$ then $0^{\circ }<\theta <45^{\circ }$

Now $\csc ^{2}2\theta =1+\cot ^{2}2\theta =1+\frac{16}{9}=\frac{25}{9}\Longrightarrow \csc 2\theta =\frac{5}{3}$

$\sin 2\theta =\frac{3}{5}$and $\cos 2\theta =\frac{4}{5}$ therefore

$\sin \theta =\sqrt{\frac{1-\cos 2\theta }{2}}=\sqrt{\frac{1-\frac{4}{5}}{2}}\qquad \cos \theta =\sqrt{\frac{1+\cos 2\theta }{2}}=$ $\sqrt{\frac{1+\frac{4}{5}}{2}}$
so
$\sin \theta =\frac{1}{10}\sqrt{10}\qquad \cos \theta =\frac{3}{10}\sqrt{10}$

and now we use the rotation equations

$x=x' \cos \theta -y' \sin \theta =\frac{3}{10}\sqrt{10}% x' -\frac{1}{10}\sqrt{10}y' $

$y=x' \sin \theta +y' \cos \theta =\frac{1}{10}\sqrt{10}x' +\frac{3}{10}\sqrt{10}y' $

Now we substitute in the conic equation

$5x^{2}+3xy+y^{2}=44\Longrightarrow $
$5\left( \frac{3}{10}\sqrt{10}x' -\frac{1}{10}\sqrt{10}y' \right) ^{2}+3\left( \frac{3}{10}\sqrt{10}x' -\frac{1}{10}\sqrt{10}y' \right) \left( \frac{1}{10}\sqrt{10}x' +\frac{3}{10}\sqrt{10}y' \right) +\left( \frac{1}{10}\sqrt{10}x' +\frac{3}{10}\sqrt{10}y' \right)^{2}=44$

This leads to $\frac{x'^{2}}{8}+\frac{y'^{2}}{88}=1$
So it is an ellipse.

Solution:
Answer: Parabola
$\cot 2\theta =\frac{A-C}{B}=\frac{1-1}{-2}=0$
then $\theta =45^{\circ }$

$x=x' \cos \theta -y' \sin \theta =\frac{\sqrt{2}}{2}x' -\frac{\sqrt{2}}{2}y' $

$y=x' \sin \theta +y' \cos \theta =\frac{\sqrt{2}}{2}x' +\frac{\sqrt{2}}{2}y' $

$x^{2}-2xy+y^{2}=8x+8y\Longrightarrow $
$\left( \frac{\sqrt{2}}{2}x' -\frac{\sqrt{2}}{2}y' \right) ^{2}-2\left( \frac{\sqrt{2}}{2}x' -\frac{\sqrt{2}}{2}y' \right) \left( \frac{\sqrt{2}}{2}x' +\frac{\sqrt{2}}{2}y' \right) +\left( \frac{\sqrt{2}}{2}x' +\frac{\sqrt{2}}{2}y' \right) ^{2} =8\left( \frac{\sqrt{2}}{2}x' -\frac{\sqrt{2}}{2}y' \right) +8\left( \frac{\sqrt{2}}{2}x' +\frac{\sqrt{2}}{2}y' \right) $

$\frac{1}{2}\left( x' \right) ^{2}-x' y' +\frac{1}{2}\left( y' \right) ^{2}-\left( x' \right) ^{2}+\left( y' \right)^{2}+\frac{1}{2}\left( x' \right) ^{2}+x' y' +\frac{1}{2}\left( y' \right) ^{2}=4\sqrt{2}x' $

$2\left( y' \right)^{2}=4\sqrt{2}x' \Longrightarrow \left( y' \right)^{2}=2\sqrt{2}x'$
The conic section is a parabola.

Solution:
Answer: Hyperbola

$\cot 2\theta =\frac{A-C}{B}=\frac{1-0}{-4}=\frac{1}{4}$
then $0^{\circ }<\theta <45^{\circ }$

$2\theta =\text{arccot}\frac{1}{4}= 1.3258\Longrightarrow \theta =\frac{1.3258}{2}\cdot \frac{180}{\pi }= 37.981^{\circ }$

then $\cos 37.981^{\circ }=0.788$
$\sin 37.981^{\circ }=0.615$ then
$x=x' \cos \theta -y' \sin \theta =0.788\,x' -0.615y' $

$y=x' \sin \theta +y' \cos \theta =0.615x' +0.788\,y' $

$x^{2}+4xy=16\Longrightarrow \left( 0.788\,x' -0.615y' \right)^{2}+4\left( 0.788x' -0.615y' \right) \left( 0.615x' +0.788 y' \right) =16$

$\left( 0.788\,x' \right)^{2}-0.969\,x' y' +\left(0.615y' \right) ^{2}+4(0.485x'^{2}+0.621x' y' -0.378\,x' y' $ $-0.969\,y'^{2}=16$

$(0.788^{2}+4\cdot 0.485)x'^{2}+(0.615^{2}-4\cdot 0.969)y'^{2}=16$

$2.560\,x'^{2}-3.498y'^{2}=16\Longrightarrow \frac{2.560}{16}\,x'^{2}-\frac{3.498}{16}y'^{2}=1$
The conic section is a hyperbola.

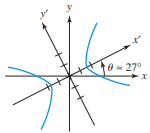
Solution:
Answer: Hyperbola

$\cot 2\theta =\frac{A-C}{B}=\frac{1+2}{-4}=\frac{3}{4}$ then $0^{\circ }<\theta <45^{\circ }$ $2\theta =\text{arccot}\frac{3}{4}=0.927\,\cdot \frac{180}{\pi }=53.\,11\Longrightarrow \theta =\frac{53.\,11}{2}\approx 27^{\circ }$

$\cos 27^{\circ }=0.891\,\qquad \sin 27^{\circ }=0.454$ then

$x=x' \cos \theta -y' \sin \theta =0.891\,x'-0.454y' $
$y=x' \sin \theta +y' \cos \theta =0.454x' + 0.891\,\,y' $
$x^{2}+4xy-2y^{2}-6=0\Longrightarrow $
$\left( 0.891\,x' -0.454y' \right) ^{2}+4\left( 0.891\,x' -0.454y' \right) \left( 0.454x' +0.891\,\,y' \right) -2\left( 0.454x' +0.891\,\,y' \right) ^{2}-6=0$

$\left( 0.891x' \right)^{2}-2\left( \left( 0.891\right) \left( 0.454\right)x' y' \right) +\left( 0.454y' \right)^{2}+4\left( \left( 0.891\right) \left( 0.454\right)x'^{2}+\left(0.891\right) ^{2}x' y' -\left( 0.454\right) ^{2}x' y' -\left( 0.891\right) \left( 0.454\right)y'^{2}\right) -2(\left( 0.454x' \right)^{2}+2\left( \left( 0.454\right) \left(0.891\right) x'y' \right) +\left( 0.891\right) y'^{2})-6=0$

After simpification, we have
$2x'^{2}-3y'^{2}=6\Longrightarrow \frac{x'^{2}}{3}-\frac{y'^{2}}{2}=1$
The conic section is a hyperbola.