Derivatives: Problems with Solutions

Solution:
Answer: $f\prime (x)=\underset{h\rightarrow 0}{\lim }\frac{f(x+h)-f(x)}{h}$

Solution:
$f\prime (x)=\underset{h\rightarrow 0}{\lim }\frac{f(x+h)-f(x)}{h}=\underset{h\rightarrow 0}{\lim }\frac{\left( x+h\right) ^{3}-12\left( x+h\right) -\left( x^{3}-12x\right) }{h}=\underset{h\rightarrow 0}{\lim }\frac{x^{3}+3x^{2}h+3xh^{2}+h^{3}-12x-12h-x^{3}+12x}{h}$

$f\prime (x)=\underset{h\rightarrow 0}{\lim }\frac{ 3x^{2}h+3xh^{2}+h^{3}-12h}{h}=\underset{h\rightarrow 0}{\lim }\frac{h\left( 3x^{2}+3xh+h^{2}-12\right) }{h}=\underset{h\rightarrow 0}{\lim }\left( 3x^{2}+3xh+h^{2}-12\right) $

$f\prime (x)=3x^{2}-12$

Solution:
$f\prime (x)=\underset{h\rightarrow 0}{\lim }\frac{f(x+h)-f(x)}{h}=\underset{h\rightarrow 0}{\lim }\frac{\sqrt{x+h+4}-\sqrt{x+4}}{h}=$

We rationalize the binomial of the square roots in the numerator

$f\prime (x)=\underset{h\rightarrow 0}{\lim }\frac{\sqrt{x+h+4}-\sqrt{x+4}}{h}=\underset{h\rightarrow 0}{\lim }\frac{\sqrt{x+h+4}-\sqrt{x+4}}{h}\cdot \frac{\sqrt{x+h+4}+\sqrt{x+4}}{\sqrt{x+h+4}+\sqrt{x+4}}$

Apply in the numerator the notable product $\left( a+b\right) \left(a-b\right) =a^{2}-b^{2}$

So, $f\prime (x)=\underset{h\rightarrow 0}{\lim }\frac{\left( \sqrt{x+h+4}\right) ^{2}-\left( \sqrt{x+4}\right) ^{2}}{h\left( \sqrt{x+h+4}+\sqrt{x+4}\right) }=\underset{h\rightarrow 0}{\lim }\frac{x+h+4-x-4}{h\left( \sqrt{x+h+4}+\sqrt{x+4}\right) }=\underset{h\rightarrow 0}{\lim }\frac{h}{h\left( \sqrt{x+h+4}+\sqrt{x+4}\right) }$
and we simplify $h.\Longrightarrow f\prime (x)=\underset{h\rightarrow 0}{\lim }\frac{1}{\left( \sqrt{x+h+4}+\sqrt{x+4}\right) }=\frac{1}{2\sqrt{x+4}}$

$f\prime (x)=\frac{1}{2\sqrt{x+4}}$

Solution:
The line tangent to the graph of a function $f(x),$ at point $(x_{0},y_{0})$

has the equation $y-y_{0}=f'(x_{0})(x-x_{0})$

$f'(x)=2x+3\Longrightarrow f'(-2)=2\left( -2\right) +3=-1 $
So $y-y_{0}=f'(x_{0})(x-x_{0})\Longrightarrow y-2=-1(x+2)\Longrightarrow y+x=0$

is the tangent line.

Solution:
The tangent to the graph of the function $f(x),$ at the point $(x_{0},y_{0})$

has equation $y-y_{0}=f\prime (x_{0})(x-x_{0})$

$f'(x)=2x+3\Longrightarrow f' (-2)=2\left( -2\right)+3=-1$ So

$y-y_{0}=f\prime (x_{0})(x-x_{0})\Longrightarrow y-2=-1(x+2)\Longrightarrow y+x=0$ is the tangent line.

Solution:
The slope of $3x-y-4=0$ is $m=3$, since the tangent is parallel to this line, then the slopes are equals, so if
$y=mx+b=3x+b$

$y=3x+b$ is the form of tangent line, we must find $b$

Let $(x_{0},y_{0})$ be the point of tangency, that is common to the line and the function.

Then $3=m=f'(x_{0})\Longrightarrow 3x_{0}^{2}=3\Longrightarrow x_{0}=\pm 1$

After substituting in the function
we have $y_{1}=3\qquad y_{2}=1$
then the possible tangency points are $(1,3)$ and $(-1,1)\Longrightarrow b=y-3x=3-3=0$ or $b=1+3=4$

There are two solutions $\left\{ \begin{array}{c} L_{1}:y=3x \\ L_{2}:y=3x+4 \end{array} \right\}$

Solution:
$f'(x)=\underset{h\rightarrow 0}{\lim }\frac{f(x+h)-f(x)}{h}=\textbf{\ }\underset{h\rightarrow 0}{\lim }\frac{\left( \left( x+h\right)^{3}+2\left( x+h\right) ^{2}-1\right) -\left( x^{3}+2x^{2}-1\right) }{h}$

$f'(x)=\underset{h\rightarrow 0}{\lim }\frac{\left( \left(x^{3}+3x^{2}h+3xh^{2}+h^{3}\right) +2\left( x^{2}+2xh+h^{2}\right) -1\right) -\left( x^{3}+2x^{2}-1\right) }{h}$

$f'(x)=\underset{h\rightarrow 0}{\lim }\frac{x^{3}+3x^{2}h+3xh^{2}+h^{3}+2x^{2}+4xh+2h^{2}-1-x^{3}-2x^{2}+1}{h}=\underset{h\rightarrow 0}{\lim }\frac{3x^{2}h+3xh^{2}+h^{3}+4xh+2h^{2}}{h}$

$f'(x)=\underset{h\rightarrow 0}{\lim }\frac{h(3x^{2}+3xh+h^{2}+4x+2h)}{h}=\underset{h\rightarrow 0}{\lim}(3x^{2}+3xh+h^{2}+4x+2h)=3x^{2}+4x$

Then $f'(c)=f'(-2)=3\left( -2\right) ^{2}+4\left(-2\right) =12-8=4$

Answer: $f'(c)=4$

Solution:
We know that $f\prime (x)=\left\{ \begin{array}{c} 1\quad \qquad x\leq 1 \\ 2x\quad \ \ \quad x>1 \end{array} \right\} $

$f'(0)=1$

Solution:
$f' (x)=\left\{ \begin{array}{c} 2x\quad \qquad x\leq 2 \\ 4\quad \ \ \quad x>2% \end{array}% \right\} \Longrightarrow f' (3)=4$

Solution:
$f\prime (t)=\frac{d}{dt}t^{3}+\frac{d}{dt}5t^{2}-\frac{d}{dt}3t+\frac{d}{dt}8=3t^{2}+5\frac{d}{dt}t^{2}-3\frac{d}{dt}t+0$

$f\prime (t)=3t^{2}+10t-3$

Solution:
$(i)$ $f(x)=x^{2}+1\Longrightarrow f'(x)=\frac{d}{dx}x^{2}+\frac{d}{dx}1=2x$ - true

$(ii)$ $g(x)=\frac{x-1}{1-x}=\frac{x-1}{-(x-1)}=-1\Longrightarrow g'(x)=0$ - false

$(iii)$ we use the chain rule.

$h(x)=\sqrt{x^{3}-x}\quad \Longrightarrow h'(x)=\frac{d/dx\left( x^{3}-x\right) }{2\sqrt{x^{3}-x}\quad }=\frac{3x^{2}-1}{2\sqrt{x^{3}-x}\quad }$ - true

Solution:
Answer: $(i),(ii)$ and $(iii)$ are false

$(i)$ we use the chain rule $f(x)=\sin (x^{3}-x+1)\Longrightarrow $

$f'(x)=\sin (x^{3}-x+1)\cdot \frac{d}{dx}(x^{3}-x+1)=\sin (x^{3}-x+1)\cdot (3x^{2}-1)$

$(i)$ is false

$(ii)$ $g(x)=e^{x^{3}+x^{2}}$ using the chain rule

$g' (x)=\frac{d}{dx}(x^{3}+x^{2})e^{x^{3}+x^{2}}$

$g' (x)=(3x^{2}+2x)e^{x^{3}+x^{2}}$ $(ii)$ - false

$(iii)$ $h(x)=\sqrt{\ln (x^{3}+1)}$ using the chain rule $h' (x)=\frac{d/dx(\ln (x^{3}+1))}{2\sqrt{\ln (x^{3}+1)}}$

$h' (x)=\frac{d/dx(\ln (x^{3}+1))}{2\sqrt{\ln (x^{3}+1)}}=\frac{d/dx(x^{3}+1)}{2(x^{3}+1)\sqrt{\ln (x^{3}+1)}}=\frac{3x^{2}}{2(x^{3}+1)\sqrt{\ln (x^{3}+1)}}$

$(iii)$ is false

Solution:
$\frac{d}{dx}(f(x)+g(x)=\frac{d}{dx}f(x)+\frac{d}{dx}g(x)=\frac{d}{dx}(\frac{1}{x}-\sin (x^{2}))+\frac{d}{dx}(x^{2}+\cos (2x+1))$

$\frac{d}{dx}(f(x)+g(x)=-\frac{1}{x^{2}}-\cos (x^{2})\frac{d}{dx}% x^{2}+2x-\sin (2x+1)\frac{d}{dx}(2x+1)=\frac{d}{dx}(f(x)+g(x)=-\frac{1}{x^{2}}-2x\cos (x^{2})+2x-2\sin (2x+1)=2x-\frac{1}{x^{2}}-2(x\cos (x^{2})+\sin (2x+1))$

Answer:

$\frac{d}{dx}(f(x)+g(x)=2x-\frac{1}{x^{2}}-2(x\cos (x^{2})+\sin(2x+1))$

Solution:
Apply product rule.

$\frac{d}{dx}(f(x)\cdot g(x))=g(x)\frac{d}{dx}f(x)+f(x)\frac{d}{dx}g(x)$

$\frac{d}{dx}(e^{x^{2}+x}\cdot \sqrt{x^{2}-x+1})=\sqrt{x^{2}-x+1}\frac{d}{dx}e^{x^{2}+x}+e^{x^{2}+x}\frac{d}{dx}\sqrt{x^{2}-x+1}$

Apply chain rule.

$\frac{d}{dx}(e^{x^{2}+x}\cdot \sqrt{x^{2}-x+1})=\sqrt{x^{2}-x+1}e^{x^{2}+x}\frac{d}{dx}\left( x^{2}+x\right) +e^{x^{2}+x}\frac{d/dx\left( x^{2}-x+1\right) }{2\sqrt{x^{2}-x+1}}$

$\frac{d}{dx}(e^{x^{2}+x}\cdot \sqrt{x^{2}-x+1})=$ $\left( 2x+1\right) \sqrt{x^{2}-x+1}e^{x^{2}+x}\frac{d}{dx}+\frac{\left( 2x-1\right) }{2\sqrt{x^{2}-x+1}}e^{x^{2}+x}$

$\frac{d}{dx}(e^{x^{2}+x}\cdot \sqrt{x^{2}-x+1})=e^{x^{2}+x}\left[ \left(2x+1\right) \sqrt{x^{2}-x+1}+\frac{\left( 2x-1\right) }{2\sqrt{x^{2}-x+1}}\right] $

Solution:
Apply division rule:
$\frac{d}{dx}(\frac{f(x)}{g(x)})=\frac{g(x)\frac{d}{dx}f(x)-f(x)\frac{d}{dx}g(x)}{g^{2}(x)}$

$\frac{d}{dx}(\frac{f(x)}{g(x)})=\frac{\ln (x^{2}-x+1)\frac{d}{dx}\left( \sqrt{2x^{3}-3x^{2}+5}\right) -\sqrt{2x^{3}-3x^{2}+5}\frac{d}{dx}\ln (x^{2}-x+1)}{\ln ^{2}(x^{2}-x+1)}$

Apply chain rule.

$\frac{d}{dx}(\frac{f(x)}{g(x)})=\frac{\ln (x^{2}-x+1)\left( \frac{d/dx(2x^{3}-3x^{2}+5)}{2\sqrt{2x^{3}-3x^{2}+5}}\right) -\sqrt{2x^{3}-3x^{2}+5}\frac{2x-1}{x^{2}-x+1}}{\ln ^{2}(x^{2}-x+1)}=\frac{d}{dx}(\frac{f(x)}{g(x)})=\frac{\ln (x^{2}-x+1)\left( \frac{6x^{2}-6x}{2\sqrt{2x^{3}-3x^{2}+5}}\right) -\sqrt{2x^{3}-3x^{2}+5}\frac{2x-1}{x^{2}-x+1}}{\ln ^{2}(x^{2}-x+1)}$

Solution:
If the line $y=5x-4$ is tangent to the graph then the slope $m=f'(x_{0})=5$

where $(x_{0},y_{0})$ is the tangent point.

$f'(x_{0})=2x_{0}-k$

$2x_{0}-k=5$
Since $(x_{0},y_{0})$ belongs to the line and the parabola we get that $y_{0}=5x_{0}-4$ and $y_{0}=x_{0}^{2}-kx_{0}$. We have the following system
$\left\{ \begin{array}{c} 2x_{0}-k=5 \\ y_{0}=5x_{0}-4 \\ y_{0}=x_{0}^{2}-kx_{0} \end{array}\right\} $ From the first equation $k=2x_{0}-5$
and we sustitute in the third equation $y_{0}=x_{0}^{2}-\left(2x_{0}-5\right) x_{0}=x_{0}^{2}-2x_{0}^{2}+5x_{0}$

The system is now reduced to two nonlinear equations $\left\{ \begin{array}{c} y_{0}=5x_{0}-4 \\ y_{0}=-x_{0}^{2}+5x_{0} \end{array} \right\} \Longrightarrow -x_{0}^{2}+5x_{0}=5x_{0}-4\Longrightarrow x_{0}^{2}=4\Longrightarrow x_{0}=\pm 2$

$k=2x_{0}-5$

$k=\pm 4-5\qquad $then $k=-1$ or $k=-9$

Solution:
Since the line $y=4x-1$ is tangent to the graph the slope $m=f'(x_{0})=4$ where $(x_{0},y_{0})$ is the tangency point $f'(x_{0})=4kx_{0}^{3}$ then

$4kx_{0}^{3}=4$
Since the point $(x_{0},y_{0})$ belongs to the line and the function we obtain that $y_{0}=4x_{0}-1$ and $y_{0}=kx_{0}^{4}$.

We get the following system
$\left\{ \begin{array}{c} 4kx_{0}^{3}=4 \\ y_{0}=4x_{0}-1 \\ y_{0}=kx_{0}^{4} \end{array} \right\}$
After eliminating $k$ from the first and third equations
$k=\frac{1}{x_{0}^{3}}\Longrightarrow y_{0}=\frac{1}{x_{0}^{3}}x_{0}^{4}=x_{0}$
We obtain the following system

$\left\{ \begin{array}{c} y_{0}=x_{0} \\ y_{0}=4x_{0}-1 \end{array} \right\} \Longrightarrow x_{0}=4x_{0}-1\Longrightarrow 3x_{0}=1\Longrightarrow x_{0}=\frac{1}{3}$

So $k=\frac{1}{\left( \frac{1}{3}\right)^{3}}=27$

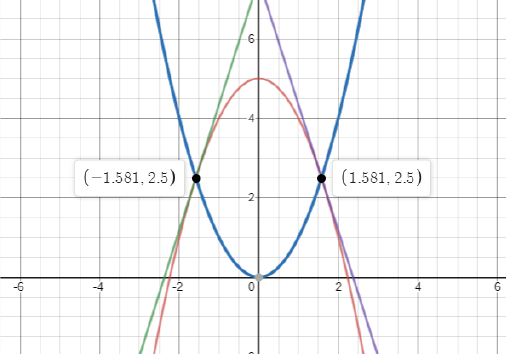
Solution:
First we find the points of intersection of the both parabolas.

$y=x^{2}$, $y=-x^{2}+5\Longrightarrow -x^{2}+5=x^{2}\Longrightarrow 2x^{2}=5$

$x_{0}=\pm \sqrt{\frac{5}{2}}=\pm 1.581\,\Longrightarrow y_{0}=x_{0}^{2}=\frac{5}{2}=2.5$

Then $\left( x_{0},y_{0}\right) =\left( \pm 1.581,2.5\right)$ are the points of intersection.

We find the slope at $\left( -1.581,2.5\right)$ point
$y' =\frac{d}{dx}\left( -x^{2}+5\right) $

$y' =-2x\Longrightarrow m=-2\left( -1.581\right) =3.162$

The equation of $L_{1}$ is
$y-y_{0}=m(x-x_{0})\Longrightarrow y-y_{0}=m(x-x_{0})\Longrightarrow y-2.5=3.162(x+1.581)$

$y-3.162x=2.5+3.162\cdot 1.581=7.5$
$L_{1}:y-3.162x=7.5$

We find the slope at the point $\left( 1.581,2.5\right)$, $y' =\frac{d}{dx}\left( -x^{2}+5\right) $
$y' =-2x\Longrightarrow m=-2\left( 1.581\right) =-3.162$

So the equation of $L_{2}$ is
$y-y_{0}=m(x-x_{0})\Longrightarrow y-y_{0}=m(x-x_{0})\Longrightarrow y-2.5=-3.162(x-1.581)$

$y+3.162x=2.5+3.162\cdot 1.581=7.5$
$L_{2}:y+3.162x=7.5$

Solution:
a) The function of position is $s(t)=-16t^{2}+v_{0}t+1362$ since that object is in free fall $v_{0}=0$ then $s(t)=-16t^{2}+1362$ is the function of position for the coin. The function of the speed is obtained by the derivative
$V(t)=\frac{d}{dt}s(t)=-32t\Longrightarrow V(t)=-32t $

b) The average speed in the range $\left[ 1,2\right] $ is
$V(2)-V(1)=-32(2)+32(1)=-32\frac{ft}{\sec }$

c) The instant speed when $t=1,t=2$ $V(1)=-32(1)=-32\frac{ft}{\sec }\qquad V(2)=-32(2)=-64\frac{ft}{\sec }$

d) When the coin is reaching the floor $s(t)=0$. So we must solve $s(t)=-16t^{2}+1362=0$ then $16t^{2}=1362\Longrightarrow t^{2}=\frac{1362}{16}=85.125\Longrightarrow t=\sqrt{85.125}$
$t=9.226\,\sec $

e) The speed when the coin is reaching the floor $V(9.226)=-32(9.226)=-295.23\frac{ft}{\sec }$

Solution:
Since $s_{0}=200$ and $v_{0}=-22ft/\sec $
The position is given by $s(t)=-16t^{2}+v_{0}t+s_{0}=-16t^{2}-22t+200$

If we calculate the function of the speed $V(t)=\frac{d}{dt}s(t)=-32t-22$

Then $V_{1}=V(3)=-32(3)-22= -118ft/\sec $
Now after descending $108$ $ft$ the position is $s(t)=200-108=92ft$

then we must solve $-16t^{2}-22t+200=92$

$-16t^{2}-22t+108=0\Longrightarrow t=\frac{22\pm \sqrt{22^{2}-4\cdot (-16)\cdot (108)}}{-32}=\frac{22-86.0}{-32}= 2$
then we calculate the speed in $2$nd $\sec \Longrightarrow V(2)=-32\left( 2\right) -22= -86ft/\sec $ $V_{2}=-86ft/\sec $

Solution:
We have that $s_{0}=0$ and $V_{0}=120m/s$ So, $s(t)=-4.9t^{2}+120t$

We calculate the speed function $V(t)=\frac{d}{dt}s(t)=-9.8t+120$
The velocity in $5$th second is $V_{5}=$ $V(5)=-9.8\left( 5\right) +120=71m/s$

The velocity in $10$th second is $V_{10}=$ $V(10)=-9.8\left( 10\right) +120=22m/s$