Vectores

Los vectores pueden representarse gráficamente por segmentos de línea dirigida. La longitud se elige, de acuerdo con alguna escala, para representar la magnitud del vector, y la dirección del segmento de línea dirigida representa la dirección del vector. Por ejemplo, si establecemos que 1 cm represente 5 km / h, entonces un viento de 15 km / h desde el noroeste estaría representado por un segmento de línea dirigida de 3 cm de largo, como se muestra en la figura de la izquierda.

Un vector en el plano es un segmento de línea dirigida. Dos vectores son equivalentes si tienen la misma magnitud y dirección.

Considere un vector dibujado desde el punto A hasta el punto B. El punto A se llama punto inicial u origen del vector, y el punto B se denomina punto final o extremo. La notación simbólica para este vector es (léase "vector AB"). Los vectores también se denotan mediante letras en negrita como u, v y w. Los cuatro vectores en la figura de la izquierda tienen la misma longitud y dirección. Así, representan vectores equivalentes; es decir,
        
En el contexto de los vectores, usamos = para significar que son equivalentes.

La longitud, o magnitud, de se expresa como ||. Para determinar si los vectores son equivalentes, encontramos sus magnitudes y direcciones.

Ejemplo 1 Los vectores u, , y w se muestran en la figura de abajo. Se muestra que u = = w.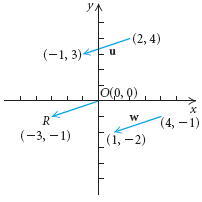

Solución Primero encontramos la longitud de cada vector usando la fórmula de distancia:
|u| = √[2 - (-1)]² + (4 - 3)² = √9 + 1 = √10,
|| = √[0 - (-3)]² + [0 - (-1)]² = √9 + 1 = √10,
|w| = √(4 - 1)² + [-1 - (-2)]² = √9 + 1 = √10.
Así
|u| = | = |w|.
Los vectores u, ,y w parece que van en la misma dirección por lo que comprobamos sus pendientes. Si las líneas en las que se encuentran tienen la misma pendiente, los vectores tienen la misma dirección. Calculemos las pendientes:
Dado que u, , y w tienen la misma magnitud y la misma dirección,
u = = w.

Tenga en cuenta que la equivalencia de los vectores requiere solo la misma magnitud y la misma dirección, no la misma ubicación. En las ilustraciones de la izquierda, cada uno de los tres primeros pares de vectores no es equivalente. El cuarto conjunto de vectores es un ejemplo de equivalencia.

Supongamos que una persona da 4 pasos al este y luego 3 pasos al norte. Luego estará a 5 pasos del punto de inicio en la dirección que se muestra a la izquierda. Un vector de 4 unidades de largo y apuntando a la derecha representa 4 pasos al este y un vector de 3 unidades de largo y apuntando hacia arriba representa 3 pasos al norte. La suma de los dos vectores es el vector 5 pasos en magnitud y en la dirección mostrada. La suma también se llama resultante de los dos vectores.

En general, dos vectores distintos de cero u y v pueden agregarse geométricamente al colocar el punto inicial de v en el punto terminal de u y luego encontrar el vector que tiene el mismo punto inicial que u y el mismo punto terminal que v, como se muestra en La siguiente figura.

La suma es el vector representado por el segmento de línea dirigido desde el punto inicial A de u hasta el punto terminal C de v. Es decir, si u= y v = , entonces
u + v = + =

También podemos describir la suma de vectores colocando los puntos iniciales de los vectores juntos, completando un paralelogramo y encontrando la diagonal del paralelogramo. (Vea la figura a la izquierda a continuación.) Esta descripción de la adición a veces se llama la ley del paralelogramo de la adición de vectores. La suma de vectores es conmutativa. Como se muestra en la figura a la derecha, tanto u + v como v + u están representados por el mismo segmento de línea dirigido.

Si dos fuerzas F₁ y F₂ actúan sobre un objeto, el efecto combinado es la suma, o resultante, F₁ + F₂ de las fuerzas separadas.

Ejemplo 2 Dos fuerzas de 15 newtons y 25 newtons actúan sobre un objeto en ángulo recto entre sí. Encuentre su suma, o resultante, suministrando la magnitud de la resultante y el ángulo que forma con la fuerza mayor.

Solución Hacemos un dibujo - esta vez, un rectángulo - usando v o para representar la resultante. Para encontrar la magnitud, usamos el teorema de Pitágoras:
|v|² = 15² + 25²          Aquí |v| denota la longitud, o magnitud, de v.
|v| = √15² + 25²
|v| ≈ 29,2.
Para encontrar la dirección, observe que dado que OAB es un triángulo rectángulo,
tanθ = 15/25 = 0,6.
Usando una calculadora, encontramos θ, el ángulo que forma el resultante con la fuerza mayor:
θ = tan^{- 1}(0,6) ≈ 31°
La resultante tiene una magnitud de 29,2 y hace un ángulo de 31° con la fuerza mayor.

Los pilotos deben ajustar la dirección de su vuelo cuando hay viento cruzado. Tanto el viento como las velocidades de la aeronave se pueden describir mediante vectores.

Ejemplo 3 Velocidad y dirección de una aeronave. Un avión viaja con un rumbo de 100° a una velocidad del aire de 190 km / h, mientras que un viento sopla a 48 km / h desde 220°. Encuentre la velocidad en tierra del avión y la dirección de su trayectoria, o rumbo, sobre el suelo.

Solución Primero hacemos un dibujo. El viento está representado por y el vector de velocidad del avión por . El vector de velocidad resultante es v, la suma de los dos vectores. El ángulo θ entre v y se denomina ángulo de deriva.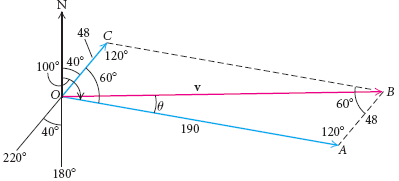

Tenga en cuenta que la medida de $\angle$COA = 100° - 40° = 60°. Así la medida de $\angle$CBAtambién es 60° (los ángulos opuestos de un paralelogramo son iguales). Dado que la suma de todos los ángulos del paralelogramo es 360° y $\angle$COB y $\angle$OAB tienen la misma medida, cada uno debe ser 120°. Por la ley de los cosenos en $\triangle$OAB, tenemos
|v|² = 48² + 190² - 2.48.190.cos120°
|v|² = 47,524
|v| = 218
Así, |v| es 218 km/h. Por la ley de los senos en el mismo triángulo,
48/senθ = 218/sen120°,
o
senθ = 48.sen120°/218 ≈ 0,1907
θ ≈ 11°
Así que, θ = 11°, redondeando al valor más cercano. La velocidad de avance del avión es de 218 km / h, y su trayectoria es en dirección a 100° - 11°, o 89°.

Dado un vector w, podemos querer encontrar otros dos vectores u y v cuya suma es w. Los vectores u y v se llaman componentes de w y el proceso de encontrarlos se llama descomposición, o representación de un vector en sus vectores componentes.

Cuando descomponemos un vector, generalmente buscamos componentes perpendiculares. La mayoría de las veces, un componente será paralelo al eje x y el otro será paralelo al eje y. Por esta razón, a menudo se les llama componentes horizontal y vertical de un vector. En la siguiente figura, el vector w = es descompuesto como la suma de u = y v = .

La componente horizontal de w es u y la componente vertical es v.

Ejemplo 4 Un vector w tiene una magnitud de 130 y está inclinado 40° con la horizontal. Descomponer el vector en sus componentes horizontal y vertical.

Solución Primero hacemos un dibujo que muestra los vectores horizontal y vertical u y v cuya suma es w.

De $\triangle$ABC, encontramos |u| y |v| usando las definiciones de las funciones coseno y seno:
cos40° = |u|/130,      o      |u| = 130.cos40° ≈ 100,
sen40° = |v|/130,      o      |v| = 130.sen40° ≈ 84.
Por lo tanto, la componente horizontal de w es 100 hacia la derecha, y la componente vertical de w es 84 hacia arriba.

Operaciones con vectores