Medidas de ángulos

Cuando dos líneas se intersecan, dan lugar a cuatro espacios diferentes con respecto al punto de intersección.
Los espacios creados se llaman ángulos.

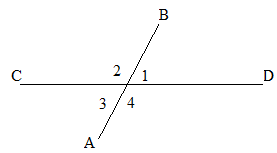
La figura muestra 4 ángulos diferentes formados en la intersección de las dos líneas AB y CD.

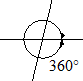
Los ángulos se miden comúnmente en grados denotados como °. Cuando un objeto se mueve a través de un ciclo completo, es decir, desde el punto D hasta el punto B, C, A y luego vuelve a D, decimos que ha cubierto 360 grados. (360°). Por lo tanto un grado es $\frac{1}{360}$ de un ciclo.

Angulos mayores a 360 grados

Hemos discutido que cuando un objeto realiza un ciclo completo alrededor de un punto, cubre 360°, sin embargo, cuando un objeto hace más de un ciclo, hace un ángulo mayor de 360 grados. Esto ocurre normalmente en la vida cotidiana. Cuando se conduce un vehículo un neumático (rueda) realiza numerosos ciclos o vueltas; por lo tanto hace un ángulo mayor que 360°.

Para averiguar el número de ciclos realizados cuando un objeto gira, contamos el número de veces que se le puede agregar 360 para obtener un número igual o menor que el ángulo dado. Del mismo modo, encontramos el número que puede multiplicarse por 360 para obtener un número menor pero más cercano al ángulo dado.

Ejemplo 2
1. Averigüe la cantidad de ciclos realizados cuando un objeto forma un ángulo de
a) 380°
b) 770°
c) 1000°
Solución
a) 380 = (1 × 360) + 20
El objeto hace un ciclo y 20°
Dado que $20^{\circ} = \frac{20}{360} = \frac{1}{18}$ ciclos
El objeto hace $1\frac{1}{18}$ ciclos.

b) 2 × 360 = 720
770 = (2 × 360) + 50
El objeto hace dos ciclos y 50°
$50^{\circ} = \frac{50}{360} = \frac{5}{36}$ ciclos
El objeto hace $2\frac{5}{36}$ ciclos
c)2 × 360 = 720
1000 = (2 × 360) + 280
$280^{\circ} = \frac{260}{360} = \frac{7}{9}$ ciclos
El objeto hace $2\frac{7}{9}$ ciclos

Ángulos positivos y negativos

Cuando un objeto gira en el sentido de las agujas del reloj, forma un ángulo negativo de rotación, mientras que cuando gira en sentido contrario a las agujas del reloj, forma un ángulo positivo. Hasta ahora, en nuestras discusiones, solo hemos estado viendo ángulos positivos.

En forma gráfica, un ángulo negativo puede ser como se muestra a continuación.

La siguiente figura muestra el signo de un ángulo medido desde una línea común, línea de 0 grados

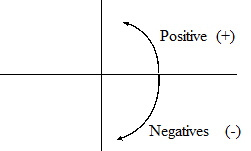
Esto implica que dado un ángulo negativo, podemos obtener su ángulo positivo respectivo.
Por ejemplo, la parte inferior de la línea vertical es 270°. Cuando se mide en la dirección negativa este será -90°. Simplemente restamos 270 de 360. Dado un ángulo negativo, sumamos 360 para obtener su ángulo positivo correspondiente.
Cuando un angulo es -360°, implica que el objeto realizó más de un ciclo en sentido horario.

Ejemplo 3
1. Encuentre el ángulo positivo correspondiente de
a) -35°
b) -60°
c) -180°
d) - 670°

2. Encuentra el ángulo negativo correspondiente de 80°, 167°, 330° y 1300°.
Solución
1. Añadimos 360 al ángulo para obtener su ángulo positivo correspondiente.
a) -35°= 360 + (-35) = 360 - 35 = 325°
b) -60°= 360 + (-60) = 360 - 60 = 300°
c) -180°= 360 + (-180) = 360 - 180 = 180°
d) -670°= 360 + (-670) = -310
Eso es un ciclo en sentido horario (360)
360 + (-310) = 50°
El ángulo es 360 + 50 = 410°

2. Restamos 360 del ángulo para obtener su ángulo negativo correspondiente.
80° = 80 - 360 = - 280°
167° = 167 - 360 = -193°
330° = 330 - 360 = -30°
1300° = 1300 - 360 = 940 (un ciclo hecho)
940 - 360 = 580 (segundo ciclo hecho)
580 - 360 = 220 (tercer ciclo hecho)
220 - 360 = -140°
El ángulo es -360 - 360 - 360 - 140 = -1220°
Así 1300° = -1220°

Radián

Un radián es un ángulo formado en el centro del círculo por un arco que es igual a la longitud del radio de ese círculo particular. Es por tanto una unidad que se utiliza para medir un ángulo. El ángulo se aproxima a 57,3°.
En la mayoría de los casos, se denota como rad.
Así 1 rad ≈ 57,3°

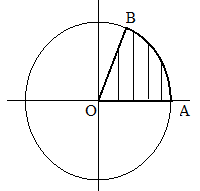
Radio = r = OA = OB = AB
Ángulo BOA es igual a 1 radián.

Dado que una circunferencia está dada por $2\pi r$ o $2\pi$ radio, por lo tanto hay $2\pi$ radianes en un ciclo completo.

Los radianes se dan comúnmente en términos de $\pi$ Para evitar tratar con decimales en los cálculos. En la mayoría de los libros, la abreviatura rad no se proporciona, pero el lector debe saber que cuando se habla de un ángulo que se da en términos de $\pi$, Las unidades son automáticamente radianes.

Algunos ángulos básicos en radianes:

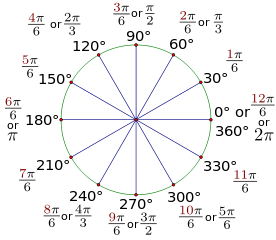
$360^{\circ} = 2\pi\ rad$
$180^{\circ} = \pi\ rad$
$90^{\circ} = \frac{\pi}{2} rad$

$30^{\circ} = \frac{30}{180}\pi = \frac{\pi}{6} rad$

$45^{\circ} = \frac{45}{180}\pi = \frac{\pi}{4} rad$

$60^{\circ} = \frac{60}{180}\pi = \frac{\pi}{3} rad$

$270^{\circ} = \frac{270}{180}\pi = \frac{27}{18}\pi = 1\frac{1}{2}\pi\ rad$

Ejemplo 4
1. Convertir 240°, 45°, 270°, 750° y 390° en radianes en términos de $\pi$.
Solución
Multiplicamos los ángulos por $\frac{\pi}{180}$.

$240^{\circ} = 240 \times \frac{\pi}{180} = \frac{4}{3}\pi=1\frac{1}{3}\pi$

$120^{\circ} = 120 \times \frac{\pi}{180} = \frac{2\pi}{3}$

$270^{\circ} = 270 \times \frac{1}{180}\pi = \frac{3}{2}\pi=1\frac{1}{2}\pi$

$750^{\circ} = 750 \times \frac{1}{180}\pi = \frac{25}{6}\pi=4\frac{1}{6}\pi$

$390^{\circ} = 390 \times \frac{1}{180}\pi = \frac{13}{6}\pi=2\frac{1}{6}\pi$

2. Convierte los siguientes ángulos en grados.
a) $\frac{5}{4}\pi$
b) $3,12\pi$
c) 2,4 radianes
Solución
$180^{\circ} = \pi$
a) $\frac{5}{4} \pi = \frac{5}{4} \times 180 = 225^{\circ}$
b) $3,12\pi = 3,12 \times 180 = 56,6^{\circ}$
c) 1 rad = 57,3°
$2,4 = \frac{2,4 \times 57,3}{1} = 137,52$

Ángulos negativos y ángulos mayores que $2\pi$ radianes

Para convertir un ángulo negativo a positivo, le sumamos $2\pi$.
Para convertir un ángulo positivo a negativo, restamos $2\pi$ de él.

Ejemplo 5
1. Convertir $-\frac{3}{4}\pi$ and $-\frac{5}{7}\pi$ a ángulos positivos en radianes.

Solución
Sumamos $2\pi$ al ángulo
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$

Cuando un objeto gira en un ángulo mayor que $2\pi$; habría realizado más de un ciclo..
Para determinar el número de ciclos de tal ángulo, debemos encontrar un número que multiplicado por $2\pi$, de como resultado un número igual o menor pero lo más cercano al ángulo.

Ejemplo 6
1. Encuentre el número de ciclos realizados cuando un objeto gira a través de los siguientes ángulos:
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$

Solución
a) $-10\pi = 5(-2\pi)$; dado que $-2\pi$ implica un ciclo en sentido de las agujas del reloj, eso implica que
el objeto hecho 5 ciclos en el sentido de las agujas del reloj.

b) $9\pi = 4(2\pi) + \pi$, $\pi =$ medio ciclo
el objeto hizo cuatro ciclos y medio en sentido contrario a las agujas del reloj.

c) $\frac{7}{2}\pi=3,5\pi=2\pi+1,5\pi$, $1,5\pi$ son tres cuartos de ciclo $(\frac{1,5\pi}{2\pi}=\frac{3}{4})$
el objeto hizo uno y tres cuartos ciclos en sentido antihorario.