Operaciones con vectores

Consideremos un vector v cuyo punto inicial es el origen en un sistema de coordenadas xy y cuyo punto terminal es (a,b). Decimos que el vector está en la posición estándar y refiere a él como un vector de posición. Tenga en cuenta que el par ordenado define el vector de forma única. Así podemos usarlo para denotar el vector. Para enfatizar que estamos pensando en un vector y para evitar la confusión de la notación con el par ordenado y la notación de intervalos, generalmente escribimos
v = < a, b >.

La coordenada a es el escalar componente horizontal del vector, y la coordenada b es el escalar componente vertical del vector. Por escalar, nos referimos a una cantidad numérica más que a una cantidad vectorial. Por lo tanto, se considera que es la forma componente de v. Tenga en cuenta que a y b NO son vectores y no deben confundirse con la definición de componente vectorial.

Ahora considere con A = (x₁, y₁) y C = (x₂, y₂). Veamos cómo encontrar el vector de posición equivalente a . Como puede ver en la siguiente figura, el punto inicial A se reubica en el origen (0, 0). Las coordenadas de P se encuentran restando las coordenadas de A de las coordenadas de C. Por lo tanto, P = (x₂ - x₁, y₂ - y₁) y el vector de posicion es .

Se puede demostrar que y tienen la misma magnitud y dirección y por lo tanto son equivalentes. Así, = = < x₂ - x₁, y₂ - y₁ >.

La forma componente de con A = (x₁, y₁) y C = (x₂, y₂) es
= < x₂ - x₁, y₂ - y₁ >.

Ejemplo 1 Encuentre la forma componente de si C = (- 4, - 3) y F = (1, 5).

Solución Tenemos
= < 1 - (- 4), 5 - (- 3) > = < 5, 8 >.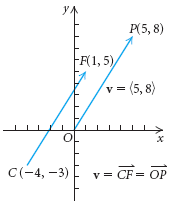

Note que el vector es equivalente al vector de posición como se muestra en la figura de arriba.

Ahora que sabemos cómo escribir vectores en su forma componente, replanteemos algunas definiciones.
La longitud de un vector v es fácil de determinar cuando se conocen los componentes del vector. Para v = < v₁, v₂ >, tenemos
|v|² = v²₁ + v²₂          Usando el teorema de Pitágoras
|v| = √v²₁ + v²₂.

La longitud, o magnitud, de un vector v = < v₁, v₂ > está dada por |v| = √v²₁ + v²₂.

Dos vectores son equivalentes si tienen la misma magnitud y la misma dirección.

Sea u = < u₁, u₂ > y v = < v₁, v₂ >. Entonces
< u₁, u₂ > = < v₁, v₂ >         si y solo si u₁ = v₁ y u₂ = v₂.

Operaciones con Vectores

Para multiplicar un vector v por un número real positivo, multiplicamos su longitud por el número. Su dirección sigue siendo la misma. Cuando un vector v se multiplica por 2, por ejemplo, su longitud se duplica y su dirección no cambia. Cuando un vector se multiplica por 1,6, su longitud aumenta en 60% y su dirección sigue siendo la misma. Para multiplicar un vector v por un número real negativo, multiplicamos su longitud por el número e invertimos su dirección. Cuando un vector se multiplica por -2, su longitud se duplica y su dirección se invierte. Como los números reales funcionan como factores de escala en la multiplicación de vectores, los llamamos escalares y los productos kv se llaman múltiplos escalares de v.

Para un número real k y un vector v = < v₁, v₂ >, el producto escalar de k y v es
kv = k.< v₁, v₂ > = < kv₁, kv₂ >.
El vector kv es un múltiplo escalar del vector v.

Ejemplo 2 Sea u = < - 5, 4 > y w = < 1, - 1 >. Encontrar - 7w, 3u, y - 1w.

Solución
- 7w = - 7.< 1, - 1 > = < - 7, 7 >,
3u = 3.< - 5, 4 > = < -15, 12 >,
- 1w = - 1.< 1, - 1 > = < - 1, 1 >.

Ahora podemos sumar dos vectores usando sus componentes. Para sumar dos vectores dados en forma componente, sumamos los correspondientes componentes. Sea u = < u₁, u₂ > y v = < v₁, v₂ >. Entonces
u + v = < u = < u₁ + v₁, u₂ + v₂ >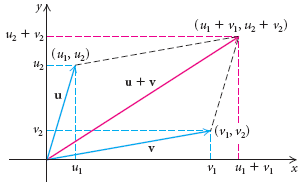

Por ejemplo, si v = < - 3, 2 > y w = < 5, - 9 >, entonces
v + w = < - 3 + 5, 2 + (- 9) > = < 2, - 7 >

Si u = < u₁, u₂ > y v = < v₁, v₂ >, entonces
u + v = < u₁ + v₁, u₂ + v₂ >.

Antes de definir la resta vectorial, necesitamos definir - v. El opuesto de v = < v₁, v₂ >, mostrado a continuación, es
- v = (- 1).v = (- 1)< v₁, v₂ > = < - v₁, - v₂ >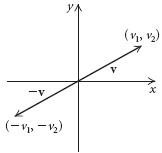

La resta de vectores como u - v implica restar los componentes correspondientes. Mostramos esto reescribiendo u - v como u + (- v). Si u = < u₁, u₂ > y v = < v₁, v₂ >, entonces
u - v = u + (- v) = < u₁, u₂ > + < - v₁, - v₂ > = < u₁ + (- v₁), u₂ + (- v₂) > = < u₁ - v₁, u₂ - v₂ >

Podemos ilustrar la resta de vectores con paralelogramos, tal como hicimos la suma de vectores.

Resta de vectores

Si u = < u₁, u₂ > y v = < v₁, v₂ >, entonces
u - v = < u₁ - v₁, u₂ - v₂ >.

Es interesante comparar la suma de dos vectores con la diferencia de los mismos dos vectores en el mismo paralelogramo. Los vectores u + v y u - v son las diagonales del paralelogramo.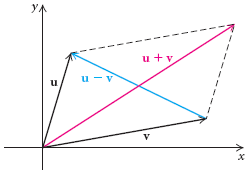

Ejemplo 3 Haga los siguientes cálculos, donde u = < 7, 2 > y v = < - 3, 5 >.
a) u + v
b) u - 6v
c)3u + 4v
d)|5v - 2u|

Solución
a) u + v = < 7, 2 > + < - 3, 5 > = < 7 + (- 3), 2 + 5 > = < 4, 7 >;
b)u - 6v = < 7, 2 > - 6.< - 3, 5 > = < 7, 2 > - < - 18, 30 > = < 25, - 28 >;
c) 3u + 4v = 3.< 7, 2> + 4.< - 3, 5 > = < 21, 6 > + < - 12, 20 > = < 9, 26 >;
d) |5v - 2u| = |5.< - 3, 5 > - 2.< 7, 2 >| = |< - 15, 25 > - < 14, 4 >| = |< - 29, 21 >| = √(- 29)² + 21² = √1282 ≈ 35,8

Antes de establecer las propiedades de la suma de vectores y la multiplicación escalar, necesitamos definir otro vector especial: el vector cero. El vector cuyos puntos inicial y terminal son ambos 0 es el vector cero, denotado por O, o < 0, 0 > . Su magnitud es 0. Además, el vector cero es el vector de identidad aditivo:
v + O = v.          < v₁, v₂ > + < 0, 0 > = < v₁, v₂ >
Las operaciones en vectores comparten muchas de las mismas propiedades que las operaciones con números reales.

Propiedades de la suma de vectores y la multiplicación escalar

Para todos los vectores u, v, y w, y para todos los escalares b y c:
1. u + v = v + u.
2. u + (v + w) = (u + v) + w.
3. v + O = v.
4 1.v = v;          0.v = O.
5. v + (- v) = O.
6. b(cv) = (bc)v.
7. (b + c)v = bv + cv.
8. b(u + v) = bu + bv.

Vector unitario

Un vector de magnitud o longitud 1 se llama vector unitario. El vector v = < - 3/5, 4/5 > es un vector unitario porque
|v| = |< - 3/5, 4/5 >| = √(- 3/5)² + (4/5)² = √9/25 + 16/25 = √25/25 = √1 = 1.

Ejemplo 4 Encuentre un vector unitario que tenga la misma dirección que el vector w = < - 3, 5 >.

Solución Primero encontramos la longitud de w:
|w| = √(- 3)² + 5² = √34. Así queremos un vector cuya longitud sea 1/√34 de w y cuya dirección es la misma que el vector w. Ese vector es
u = w/√34 = < - 3, 5 >/√34 = < - 3/√34, 5/√34 >.
El vector u es un vector unitario porque
|u| = |w/√34| = 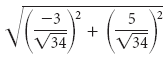= √34/34 = √1 = 1.

Si v es un vector y v ≠ O, entonces
(1/|v|)• v,          o          v/|v|,
es un vector unitario en la dirección de v.

Aunque los vectores unitarios pueden tener cualquier dirección, los vectores unitarios paralelos a los ejes x e y son particularmente útiles. Se definen como
i = < 1, 0 >          y          j = < 0, 1 >.

Cualquier vector puede ser expresado como una combinación lineal de los vectores unitarios i y j. Por ejemplo, sea v = < v₁, v₂ > entonces
v = < v₁, v₂ > = < v₁, 0 > + < 0, v₂ > = v₁< 1, 0 > + v₂ < 0, 1 > = v₁i + v₂j.

Ejemplo 5 Expresar el vector r = < 2, - 6 > como una combinación lineal de i y j.

Solución
r = < 2, - 6 > = 2i + (- 6)j = 2i - 6j.

Ejemplo 6 Escriba el vector q = - i + 7j en su forma componente.

Solución q = - i + 7j = -1i + 7j = < - 1, 7 >

Las operaciones de vectores también se pueden realizar cuando los vectores se escriben como combinaciones lineales de i y j.

Ejemplo 7 Si a = 5i - 2j y b = -i + 8j, encontrar 3a - b.

Solución
3a - b = 3(5i - 2j) - (- i + 8j) = 15i - 6j + i - 8j = 16i - 14j.

Ángulo de dirección

El punto terminal P de un vector unitario en posición estándar es un punto en el círculo unitario indicado por (cosθ, senθ). Así, el vector unitario se puede expresar en su forma componente, u = < cosθ, senθ >,
o como una combinación lineal de los vectores unitarios i y j,
u = (cosθ)i + (senθ)j,
donde los componentes de u son funciones del ángulo de dirección θ medido en sentido antihorario desde el eje x hasta el vector. Como θ varía de 0 a 2π, el punto P traza el círculo x² + y² = 1. Esto va en todas las direcciones posibles para los vectores unitarios, por lo que la ecuación u = (cosθ)i + (senθ)j describe todos los vectores unitarios posibles en el plano.

Ejemplo 8 Calcular y dibujar el vector unitario u = (cosθ)i + (senθ)j for θ = 2π/3. Incluya el círculo unitario en su esquema.

Solución
u = (cos(2π/3))i + (sen(2π/3))j = (- 1/2)i + (√3/2)j

Sea v = < v₁, v₂ > con ángulo de dirección θ. Usando la definición de la función tangente, podemos determinar el ángulo de dirección de los componentes de v: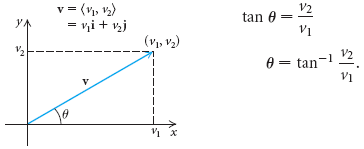

Ejemplo 9 Determine el ángulo de dirección θ del vector w = - 4i - 3j.

Solución Sabemos que
w = - 4i - 3j = < - 4, - 3 >.
Asi tenemos
tanθ = (- 3)/(- 4) = 3/4          y θ = tan^{- 1}(3/4).
Como w está en el tercer cuadrante, sabemos que θ es un ángulo del tercer cuadrante. El ángulo de referencia es
tan^{- 1}(3/4) ≈ 37°,          y          θ ≈ 180° + 37°, o 217°.

Es conveniente para el trabajo con problemas aplicados y en cursos posteriores, como el cálculo, tener una forma de expresar un vector para que tanto su magnitud como su dirección puedan determinarse o leerse fácilmente. Sea v un vector. Entonces v/|v| es un vector unitario en la misma dirección que v. Así tenemos
v/|v| = (cosθ)i + (senθ)j
v = |v|[(cosθ)i + (senθ)j]              Multiplicando por |v|
v = |v|(cosθ)i + |v|(senθ)j.

Ejemplo 10 Velocidad y dirección de un avión. Un avión viaja sobre un rumbo de 100° a una velocidad aérea de 190 km/h mientras sopla un viento de 48 km/h desde 220°. Encuentre la velocidad en tierra del avión y la dirección de su trayectoria, o rumbo, sobre el suelo.

Solución Primero hacemos un gráfico. El viento está representado por y el vector de velocidad del avión por . El vector de velocidad resultante es v, la suma de los dos vectores:
v = + .

El rumbo (medido desde el norte) del vector de velocidad aérea es 100°. Su ángulo de dirección (medido en sentido antihorario desde el eje x positivo) es 350°. El rumbo (medido desde el norte) del vector viento es 220°. Su ángulo de dirección (medido en sentido antihorario desde el eje x positivo) es 50°. Las magnitudes de y son 190 y 48, respectivamente. Tenemos
= 190(cos350°)i + 190(sen350°)j, y = 48(cos50°)i + 48(sen50°)j.
Así,
v = +
     = [190(cos350°)i + 190(sen350°)j] + [48(cos50°)i + 48(sen50°)j]
     = [190(cos350°)i + 48(cos50°)i] + [190(sen350°)j + 48(sen50°)j]
     ≈ 217,97i + 3,78j.
De esta forma, podemos determinar la velocidad de avance y el rumbo:
Velocidad sobre el suelo ≈ √(217,97)² + (3,78)² ≈ 218 km/h.
Dejemos que α sea el ángulo de dirección de v. Entonces
tanα = 3,78/217,97
α = tan^{- 1}3,78/217,97 ≈ 1°.
Así, el curso del avión (la dirección desde el norte) es 90° - 1°, o 89°.

Ángulo entre vectores

Cuando un vector se multiplica por un escalar, el resultado es un vector. Cuando se suman dos vectores, el resultado es también un vector. Por lo tanto, podríamos esperar que el producto de dos vectores sea también un vector, pero no lo es. El producto escalar de dos vectores es un número real, o escalar. Este producto es útil para encontrar el ángulo entre dos vectores y para determinar si dos vectores son perpendiculares.

El producto escalar de dos vectores u = < u₁, u₂ > y v = < v₁, v₂ > es
u • v = u₁.v₁ + u₂.v₂
(Nótese que u₁v₁ + u₂v₂ es un escalar, no un vector)

Ejemplo 11 Encuentre el producto escalar indicado cuando
u = < 2, - 5 >, v = < 0, 4 > y w = < - 3, 1 >.
a)u • w
b)w • v

Solución
a) u • w = 2(- 3) + (- 5)1 = - 6 - 5 = - 11;
b) w • v = (- 3)0 + 1(4) = 0 + 4 = 4.

El producto escalar se puede utilizar para encontrar el ángulo entre dos vectores. El ángulo entre dos vectores es el ángulo positivo más pequeño formado por los dos segmentos de línea dirigidos. Así el angulo θ entre u y v es el mismo ángulo que entre v y u, y 0 ≤ θ ≤ π.

Si θ es el ángulo entre dos vectores distintos de cero u y v, entonces
cosθ = (u • v)/|u||v|.

Ejemplo 12 Encuentre el ángulo entre u = < 3, 7 > y v = < - 4, 2 >.

Solución Comenzamos por encontrar u • v, |u|, y |v|:
u • v = 3(- 4) + 7(2) = 2,
|u| = √3² + 7² = √58, y
|v| = √(- 4)² + 2² = √20.
Entonces
cosα = (u • v)/|u||v| = 2/√58.√20
α = cos^{- 1}(2/√58.√20)
α ≈ 86,6°.

Fuerzas en equilibrio

Cuando varias fuerzas actúan a través del mismo punto en un objeto, su suma vectorial debe ser O para que se produzca un equilibrio. Cuando se produce un equilibrio, entonces el objeto está inmóvil o moviéndose en línea recta sin aceleración. El hecho de que la suma vectorial debe ser O para un balance, y viceversa, nos permite resolver muchos problemas aplicados que involucran fuerzas.

Ejemplo 13 Bloque suspendido. Un bloque de 350 libras está suspendido por dos cables, como se muestra a la izquierda. En el punto A, hay tres fuerzas que actúan: W, el bloque que tira hacia abajo y R y S, los dos cables que tiran hacia arriba y hacia afuera. Encuentre la tensión en cada cable.

Solución Dibujamos un diagrama de fuerza con los puntos iniciales de cada vector en el origen. Para que haya un balance, la suma del vector debe ser el vector O: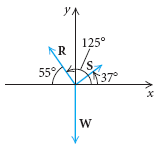

R + S + W = O.
Podemos expresar cada vector en términos de su magnitud y su ángulo de dirección:
R = |R|[(cos125°)i + (sen125°)j],
S = |S|[(cos37°)i + (sen37°)j], y
W = |W|[(cos270°)i + (sen270°)j]
= 350(cos270°)i + 350(sen270°)j
= -350j          cos270° = 0; sen270° = - 1.
Sustituyendo por R, S, y W en R + S + W + O, tenemos
[|R|(cos125°) + |S|(cos37°)]i + [|R|(sen125°) + |S|(sen37°) - 350]j = 0i + 0j.
Esto nos da un sistema de ecuaciones:
|R|(cos125°) + |S|(cos37°) = 0,
|R|(sen125°) + |S|(sen37°) - 350 = 0.
Resolviendo este sistema, obtenemos
|R| ≈ 280 y |S| ≈ 201.
Las tensiones en los cables son 280 lb y 201 lb.

Vectores