Lobachevski - Non-Euclidean Geometry
PART II
If ever there was a scandal in the intellectual world, Euclid's fifth postulate constituted such a scandal. The very existence of this postulate seemed offensive to a great many people; even those who did not completely condemn the postulate nevertheless considered it a blemish on Euclid's otherwise elegant edifice. Indeed, there exists a book by an eighteenth-century Italian Jesuit, Girolamo Saccheri, the English title of which is Euclid Freed of Every Fleck. This book, published in 1733, is not a mere curiosity written by a crank; it is a very serious work which plays an important role in the controversy surrounding the postulate. Now, however, this controversy no longer exists. The fifth postulate has become quite acceptable, and Euclid, instead of being chastised for having formulated it, is praised for having recognized the need for it. Indeed, mathematicians hold that the fifth postulate is characteristic of Euclid's geometry. It is now recognized that Saccheri and all the other mathematicians who felt uncomfortable about the fifth postulate were really searching for a form of generalized non-Euclidean geometry.
Let us take a close look at Euclid's famous—or infamous— postulate:
Let it be postulated that, if a straight line falling on
two straight lines make the interior angles on the same
side less than two right angles, the two straight lines, if
produced indefinitely, meet on that side on which are
the angles less than the two right angles (p. 17).
Whereas the first four postulates are brief and easily understood, Euclid's fifth postulate is as lengthy as a proposition and as complicated. The complication and length constitute the major objections to the postulate. Its statement begins with something that is given—the interior angles on the same side are less man two right angles—and then proceeds to a conclusion—the two lines will meet on the side where the angles are less than two right angles. (See Figure 2-1.) Objectors
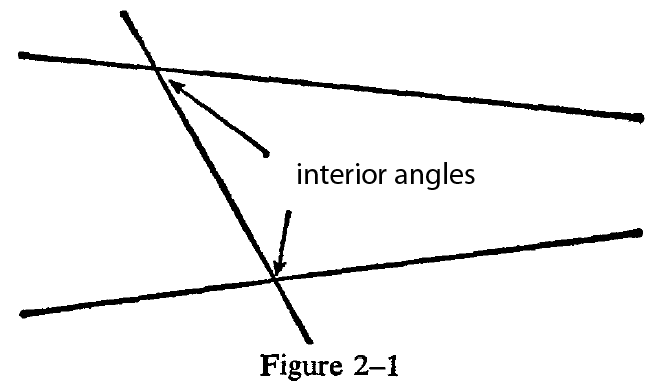
feel that it is not at all self-evident that the conclusion follows from the premises. Hence, whereas we can easily accept the validity of the first four postulates, there is no reason why we should consider the fifth postulate valid. Objectors feel that its truth should be proved, just as though it were a proposition.
The matter is worse if the postulate is called an axiom (as it frequently is in early Latin translations of Euclid), for, as we noted in Chapter I, axioms are statements of self-evident truths; but the fifth postulate is not self-evident, and so the name "axiom" should not be applied to it. Thus Saccheri, after stating the "axiom," writes as follows:
No one doubts the truth of this proposition; but...
they accuse Euclid... because he has used for it the
name axiom, as if obviously from the right understand-
ing of its terms alone came conviction. Whence not a
few (withal retaining Euclid's definition of parallels)
have attempted its demonstration from those proposi-
tions of Euclid's First Book alone which precede the
twenty-ninth, wherein begins the use of the controverted
proposition.
Here the objections and the proposed remedy are quite clearly stated. Saccheri states that the fifth postulate or axiom is true but that it is wrong to call it by the name "axiom" (that is, to claim self-evidence for it); hence the postulate must be proved to be true. To accomplish this proof, we have available to us all the propositions in Book I which precede Proposition 29, the first one in which the postulate is used. Saccheri attempts to accomplish this task, and to a certain extent he succeeds.
Nicholas Lobachevski, writing more than a hundred years after Saccheri (in 1840), employs almost the same language:
In geometry I find certain imperfections which I hold
to be the reason why this science... can as yet make
no advance from that state in which it has come to us
from Euclid.
As belonging to these imperfections, I consider ... the
momentous gap in the theory of parallels, to fill which
all efforts of mathematicians have been so far in vain
The man who wrote these words was born at Makariev, Russia, in the year 1793. Lobachevski went to the gymnasium in the city of Kazan, and then entered the university there. All of his active intellectual life was spent at the University of Kazan; he was first a student, then a professor, and finally the rector of the University. Lobachevski carried a tremendous load of teaching and administrative responsibilities (the latter being especially heavy in bureaucratic Russia), so that we wonder how he ever found time for his own research. His first writings on the subject of parallels go back to 1826, but the Theory of Parallels was not published until 1840. Incidentally, almost :he same results as those obtained by Lobachevski were found by John Bolyai, a Hungarian mathematician. His work on parallelism was published in 1831, but it is thought that Bolyai's first ideas on the subject go back to 1823. Neither Lobachev-ski's nor Bolyai's works attracted much attention when they were first published; not until 1867, when Bernhard Riemann's essay on the basic hypotheses that support geometry was posthumously published, did mathematicians generally take an interest in non-Euclidean geometries. Lobachevski died in the year 1856.
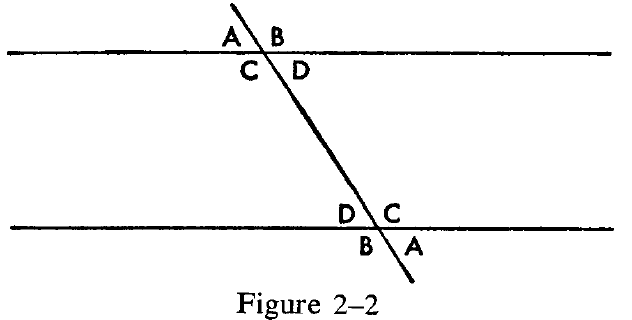
Let us begin with a look at Euclid's theory of parallels. The first proposition involving parallel lines—Proposition 27— does not make use of Postulate 5. The proposition states that, if a line intersects two other lines in such a way that the alternate angles are equal, then the two lines are parallel. (See Figure 2-2. In that figure, alternate angles are designated by the same letters.)
To prove this proposition, Euclid employs the method of reduction to the absurd: if two lines are not parallel, then of course they must meet. Assume, therefore, that they do meet (it does not matter on which side) at the point G (see Figure 2-3). A triangle, EFG, is then formed. One of the pairs of alternate angles is AEF and EFD; it is given that they are equal. However, it is impossible that they be equal, since in
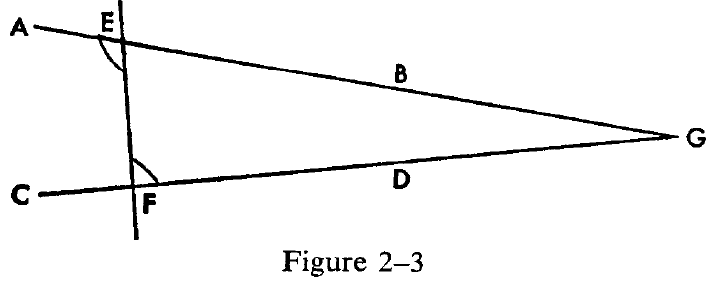
the triangle EFG the angle AEF is an exterior angle, whereas angle EFG is an interior angle. According to Proposition 16 of Book I, an exterior angle of a triangle is always greater than either of the two opposite interior angles. Hence, the same angle {AEF) must be both equal to, and greater than, EFG— a conclusion which is absurd. Thus the original assumption — that the two lines meet to form a triangle — must be false, and so the given two lines must be non-meeting or parallel.
Let us skip Proposition 28, which is just another version of Proposition 27, and hurry on to Proposition 29, in which the parallel postulate is used for the first time. Proposition 29 is the converse of Proposition 27. What is given in the first proposition becomes what is proved in the second proposition, and what is proved in the first proposition becomes what is given in the second one. Thus it is given in Proposition 27 that the alternate angles are equal, and it is proved that the two lines in question are parallel. On the other hand, in Proposition 29 it is given that the two lines are parallel, and it is proved that the alternate angles are equal.
The proof is by reduction to the absurd, just as is the proof of Proposition 27. Let us assume, Euclid says, that the alternate angles are not equal. Then one of them must be greater than the other one (it does not matter which one it is). Let the greater angle be AGH. (See Figure 2-4.) Add the angle BGH to both the angle AGH and the angle GHD. Then angle AGH + angle BGH is greater than angle GHD + angle BGH.
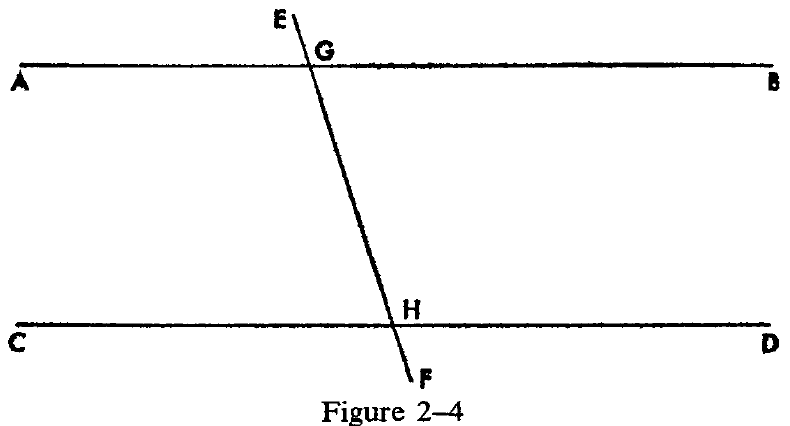
But angle AGH + angle BGH is equal to two right angles. Hence the two angles GHD + BGH are less than two right angles. And so, by Postulate 5 the lines AB and CD, if extended, must meet toward BD. However, this is absurd, since the lines are given to be parallel. And so the assumption that the alternate angles are not equal must be false.
Since Propositions 27 and 29 are converses, we should expect their proofs to be similar. And so they are: both proceed by reduction to the absurd. The element which produces the absurdity, however, is different: in the case of Proposition 27, it is Proposition 16 that is the keystone to the proof, whereas in the case of Proposition 29 it is Postulate 5 that provides the absurdity.
In order to overcome the "flaws" of Euclid's geometry, Lo-bachevski substitutes a new postulate for Euclid's fifth one. Unfortunately, he is not very explicit in his manner of doing it. To understand Lobachevski's procedure, we must first realize that there are several different but equivalent ways in which Euclid's fifth postulate can be stated. One of the equivalent statements of Postulate 5 is this: "In a plane, through a given point, there is one and just one parallel line to a given line."
To see how this statement is equivalent to Euclid's fifth postulate, let us restate the proof of Proposition 29, using the postulate of the uniqueness of the parallel line. It is to be proved that if a line intersects two parallel lines, then the alternate angles are equal. Let AB and CD be the parallel lines, and let EF intersect them. (See Figure 2-5.) It is to be proved
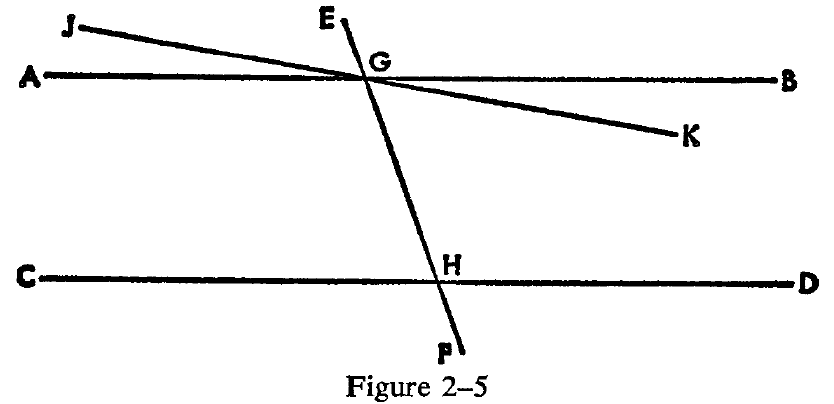
that angle AGH = angle GHD. We use reduction to the absurd. If the two angles are not equal, then construct angle JGH so that it is equal to angle GHD. Extend line JG so that the line JK is formed. Now, because of the equality of angle JGH and angle GHD, the two lines JK and CD are parallel, according to Proposition 27. But line AB is also parallel to line CD. Thus we have arrived at an absurdity—for two lines, JK and AB, are both parallel to the same line, CD. According to the postulate of the "uniqueness of parallel lines," this is impossible.
The postulate Lobachevski substitutes for Euclid's may be expressed in this form: "In a plane, through a given point, there exists an infinite number of lines that do not cut a given line." Thus Lobachevski postulates an infinite number of parallel lines to a given line, in Euclid's sense of the word "parallel." Lobachevski himself, however, reserves the term "parallel" for two special not-cutting lines.
In section 16 (p. 70) Lobachevski defines parallelism. However, he first makes a distinction:
All straight lines which in a plane go out from a point
can, with reference to a given straight line in the same
plane, be divided into two classes—into cutting and not-
cutting.
Of course, Euclid would agree with this definition, but he would add that the class of not-cutting lines has just one member, that not-cutting line being the one which Euclid calls the parallel. Lobachevski, as we have said, postulates that there is an infinite number of not-cutting lines, just as there is an infinite number of cutting lines. Parallel lines are defined by bim in terms of these two classes: "The boundary lines of the one and the other class of lines will be called parallel to the given line." If there are both not-cutting and cutting lines, there must be a last not-cutting line; that is, every line beyond this last one is such that it cuts the given line, whereas every line on the other side of this last one does not cut the given line. None of this contradicts anything that Euclid has said; it merely becomes superfluous if there is only one not-cutting line. In that case the boundary line between cutting and not-cutting lines is itself identical with the one and only not-cutting line.
Having substituted a new postulate for Euclid's—but one which is not contradictory to Euclid's, merely wider—Lobachevski proceeds to prove propositions concerning the same matters as Euclid. Naturally, his results are not the same as Euclid's; however, they are not contradictory to Euclid's. Just as Euclid's postulate is a special case of Lobachevski's postulate (that is, the special case when the not-cutting lines number only one), so Euclid's propositions are special cases of Lobachevski's. For example, Euclid finds that the sum of the angles in a triangle is equal to two right angles; Lobachevski finds this sum to be either two right angles or less than two right angles. Since Lobachevski's postulate is more complicated than Euclid's, it should not be surprising that the proofs of his propositions are also more complex.
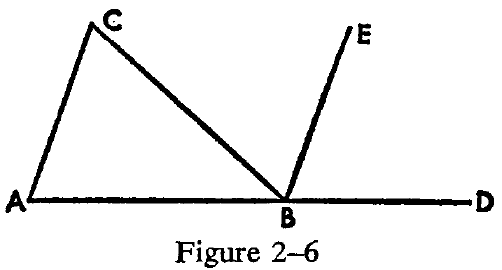
Euclid proves that the angles of a triangle are equal to two right angles in the following manner: If the triangle is ABC, Euclid first extends the line AB to D. (See Figure 2-6.) Then, through B, he draws BE parallel to AC. From Proposition 29 it follows that angle CBE is equal to angle ACB, and that EBD is equal to angle CAB. Hence the three angles ABC, CBE, and EBD are equal to the three interior angles of the triangle. But the former angles, being the angles on a straight line, are equal to two right angles; consequently the interior angles of a triangle must also be equal to two right angles. In Lobachevski's geometry this proof fails, of course, because of the unavailability of Proposition 29.
What does Lobachevski substitute for Proposition 32? In any triangle, Lobachevski tells us, the sum of the angles is at most equal to two right angles. Thus there may be triangles in which the sum of the interior angles is less than two right angles, or there may be triangles in which the sum is exactly equal to two right angles. But there are no triangles in which the sum of the angles is greater than two right angles. The proof is found in Section 19. The method used is that of reduction to the absurd. (Note that the methods of Euclid and Lobachevski are the same, even though some of their crucial assumptions are different.) Lobachevski assumes that the sum of the angles in a triangle is greater than two right angles. (For "two right angles" Lobachevski uses the expression π; this is merely a different way of measuring angles. A third way of expressing the assumption is to say that the sum of the angles of the triangles is greater than 180°. We shall adhere to Euclid's way of measuring angles—in terms of right angles.)
To arrive at an absurdity, Lobachevski bisects one of the sides of the triangle, BC, at a point D. (See Figure 2-7.) He
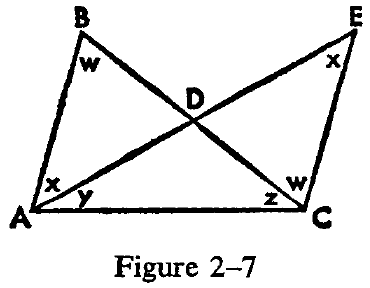
connects A and D with a straight line and extends AD to E so that AD equals DE. Then it is easy to prove that triangles ABD and DCE are congruent (this does not involve any reference to parallelism). Now consider the newly formed triangle A EC. The sum of its angles—EAC, ACE, and CEA— is equal to the sum of the angles of the original triangle. For the sake of convenience, we have given letters to the various angles. Equal angles have been designated by the same letter. In the original triangle the sum of the interior angles, starting at point B and running counterclockwise, is w + x + y + z. In the new triangle, starting at E and going counterclockwise, the sum x + y + z + w. It follows that the sum of the angles in the new triangle AEC is also greater than two right angles. If the sum of the angles in the first triangle ABC is, for example, 2 right angles + a, then it is also 2 right angles + a in the new triangle AEC. At the same time, it is clear that the angle EAC (or y) is smaller than the angle BAC (or x + y) .By proceeding in the same manner with triangle AEC (that is, by dividing the side EC in half), we arrive at yet another triangle with the sum of its angles equal to 2 right angles + a; this triangle will have an angle at A even smaller than EAC or y. By proceeding in this manner, it is possible to finally arrive at a triangle which has an angle at A smaller than the quantity a/2. We can proceed in the same manner with the other small angle (such as the one E) and, while keeping the sum of the angles in the triangle constant, have the other small angle also equal to less than a/2. Since the sum of the three angles of the final triangle must be equal to 2 right angles + a, while the two small angles together are less than a (each separately being less than a/2), the remaining third angle will have to be greater than two right angles. This is absurd, for if this third angle ever becomes so large as to be equal to two right angles, there will be no angle—and no triangle—left. We conclude, then, that the original assumption is wrong and that the sum of the angles in a triangle cannot be greater than two right angles.
In Section 20, Lobachevski points out that he does not know what the sum of the angles in a triangle amounts to, except that the sum cannot be greater than two right angles. He then adds this: if there is just one triangle concerning which it is known that the sum of its angles is exactly equal to two right angles, then all triangles must have the sum of their angles equal to two right angles. Let the triangle concerning which it is known that the sum of its angles is equal to two right angles be ABC. (See Figure 2-8.) Let MNO be any other right-angled triangle. (We are changing Lobachevki's terminology, since
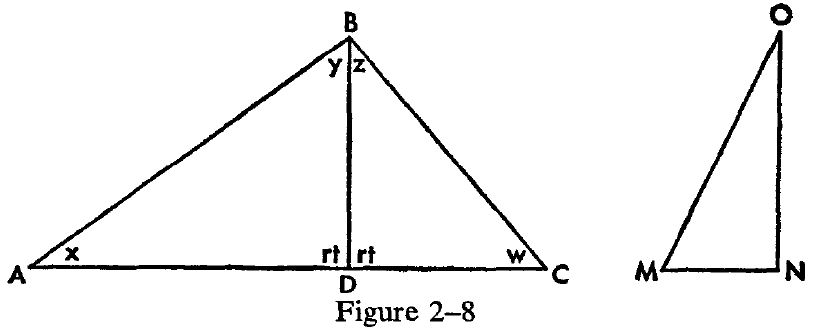
he uses the same letters in several triangles, thereby creating unnecessary confusion.) From the vertex opposite the largest side of ABC drop the perpendicular BD. This divides the triangle ABC into two right-angled triangles, ABD and BDC. From the previous proposition, the sum of the angles in either of the right-angled triangles cannot be greater than two right angles. Thus we have
(1) x + y + right angle is equal to or less than 2 right angles.
and
(2) z + w + right angle is equal to or less than 2 right angles.
If we now add these two lines together, we get
(3) x + y + z + w + 2 right angles is equal to or less than 4 right angles.
But since it is given that x + y + z + w is equal to 2 right angles, it is clear that in statement (3) the relation of being "equal" rather than that of being "less than" holds. In other words, statement (3) should be written as follows:
(3) x + y +z + w + 2 right angles = 4 right angles.
Therefore, in lines (1) and (2), we must also have the relation of equality; for if in either of them the relation of being "less than" obtained, we could not by adding obtain line (3) with the equal sign. Thus triangle BDC has the sum of its angles equal to two right angles, as does triangle ADB. By placing two triangles such as BDC together, we can form a rectangle (Lobachevski uses the term "quadrilateral") with sides BC = p, and DC = q. From many rectangles equal to this one, we can form one with sides np and nq, where n is a whole number. (Lobachevski says to make the rectangle with sides np and mq, where n and m are different whole numbers; however, he then is not entitled to take the following step,
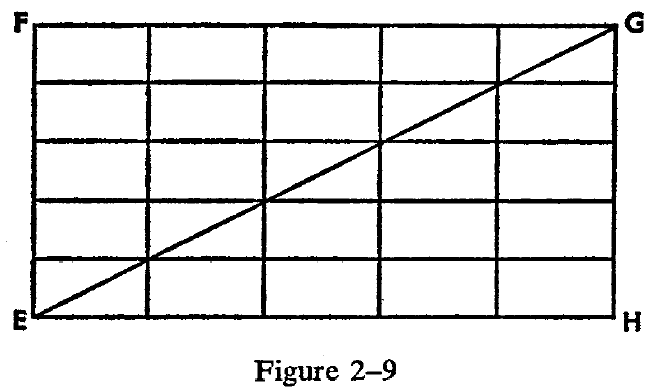
although he seems unaware of it.) Let this large rectangle be called EFGH. (See Figure 2-9.) The diagonal EG divides this rectangle into two congruent triangles, EFG and EGH. The sum of the angles in each of these two big triangles is equal to
 two right angles, because the angles of the big triangles are equal to the angles of the original triangle BDC with the sides p and q.
two right angles, because the angles of the big triangles are equal to the angles of the original triangle BDC with the sides p and q.
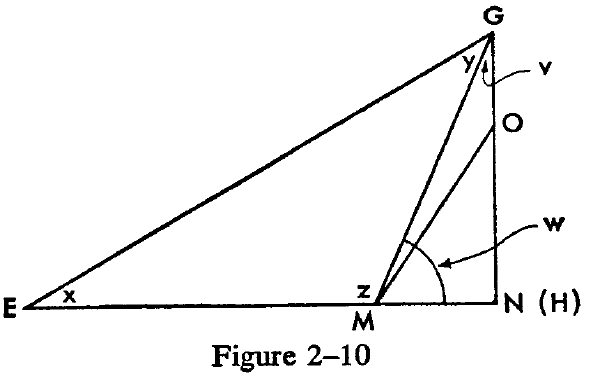
Now choose the number n large enough so that EH is greater than MN and GH is greater than NO. Draw the triangle EGH so that it wholly encloses the triangle MNO. (See Figure 2-10.) Thus points H and N coincide. Join M and G. We shall now show that, since the big triangle, EGH, has angles equal to two right angles, the two triangles which together make it up—EGM and MGN—must each have angles equal to two right angles. Similarly, since the sum of the angles in MGN is equal to two right angles, the angles in triangle MNO must amount to the same sum.
We already know that the angles of any triangle must be either less than two right angles or exactly equal to two right angles. But if the angles x + y + z are less than two right angles or if the angles w + v are less than a right angle (it is given that the angle at N is right), an impossibility results. For if we add all these angles up, we find that x + y + v + z + w are less than three right angles. Now it is known from Euclid's Proposition 13 that z + w is equal to two right angles. That would leave x + y + v as equal to less than one right angle. But this cannot be, since these three angles, together with the right angle at N, are supposed to make two right angles. Thus our assumption has led to an absurdity, and we see that all the triangles enclosed in EGH must have their angles equal to two right angles.
Since MNO was any right triangle, we can conclude that if any right triangle has the sum of its interior angles equal to two right angles, then all right triangles have their angular sum equal to two right angles. If all right triangles have their angular sum equal to two right angles, then all triangles have the same angular sum, for any triangle can be divided into two right triangles.
From this Lobachevski concludes that "only two hypotheses are allowable: Either is the sum of the three angles in all rectilineal triangles equal to π [two right angles], or this sum is in all less than π." In other words, either all geometry is Euclidean, or all geometry is Lobachevskian. There cannot be a mixture of the two geometries. "It follows," Lobachevski writes,
that in all rectilineal triangles the sum of the three
angles is either π [two right angles]..., or for all tri-
angles this sum is less than π....
The first assumption serves as the foundation for the ordinary geometry and plane trigonometry.
The second assumption can likewise be admitted without leading to any contradiction in the results, and founds a new geometric science, to which I have given the name Imaginary Geometry, and which I intend here to expound... (pp. 77-8).
We have merely Lobachevski's word for the fact that his geometry can be developed without contradition; he has not proved this. At the same time, it is only fair to note that Euclid nowhere proves that his geometry will never lead to contradictions. Euclid's "proof consists in the actual development of hundreds of propositions without contradictions; Lobachevski's "proof is of the same sort. The pages following Section 22 are a verification of his boast that a non-contradictory geometry can be developed from his postulate.
Let us re-examine Section 19. This is the section in which Lobachevski proves that the sum of the angles of any triangle cannot be greater than two right angles. Compare the proof of this proposition with the proof of Euclid's sixteenth proposition, which shows that in a triangle the exterior angle is always greater than either of the two opposite interior angles. You will notice that the two proofs are almost the same. Both depend on the same construction: the side BC of the triangle ABC is bisected; A is joined to D and then extended so that AD = DE. Then E is joined to C. (See Figure 2-11.) The two triangles ABD and DEC are easily shown to be congruent Euclid and Lobachevski use this congruency for different purposes.
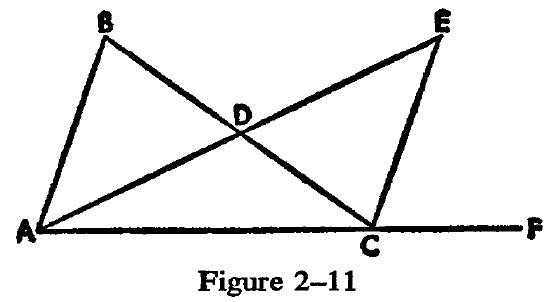
Euclid concludes that since angle ABD is equal to angle DCE, therefore the exterior angle DCF must be greater than the interior angle ABD.
Now let us make a slight change in the diagram for Proposition 16 (of Euclid) or Section 19 (of Lobachevski). Instead of drawing the figure with straight lines, as we have so far done, let us draw the figure on the surface of a sphere. Here the place of straight lines is taken by great circles—circles that have the same center as the sphere itself. Examples of great circles on the Earth are the equator and all of the meridians. A great circle is like a straight line, in that it constitutes the shortest distance between two points on a sphere, just as a straight line is the shortest distance between two points on a plane.
Look at Figure 2-12. We have drawn a triangle ABC consisting of parts of great circles. The base AC is part of the "equator" of the sphere; the two sides AB and BC are each "meridians"; thus the point B is the "north pole" of the sphere. In order to give some definiteness to the figure, we have made the angle at B equal to 120°. (We shall here use the degree measurement of angles for simplicity's sake.) Notice that no matter what the angle at B is made to be, the two angles at A and at C are right angles. Thus no matter what the angle at B is, the sum of the angles of the triangle ABC is certainly going to be greater than two right angles or 180°. In our example, it is three and a third right angles, or 300°. Thus Loba-chevski's Section 19 does not apply to spherical triangles. If we now extend the base AC, say to F, it is also apparent at once that Euclid's Proposition 16 does not hold true for spherical triangles. For the exterior angle BCF is a right angle; it is therefore equal to one of the opposite interior angles—the one at A—and is smaller than the other opposite interior angle — the one at B.
If we complete the figure so that, on the sphere, we duplicate the constructions of Proposition 16 or Section 19, we can see why their statements cannot be proved here. Bisect BC at D. Join A and D (with a great circle), and extend the great circle segment to E so that AD = DE. Join E and C with the segment of a great circle. (It takes a little practice to see the diagram properly. The point E is on the far side of the sphere; to understand why EC is drawn the way it is, remember that the circle of which EC is a part has its center at the center of the sphere. Below the main diagram we have placed another one, in which the spherical triangle has been "flattened out" and placed in the plane. This may help in visualizing the spherical
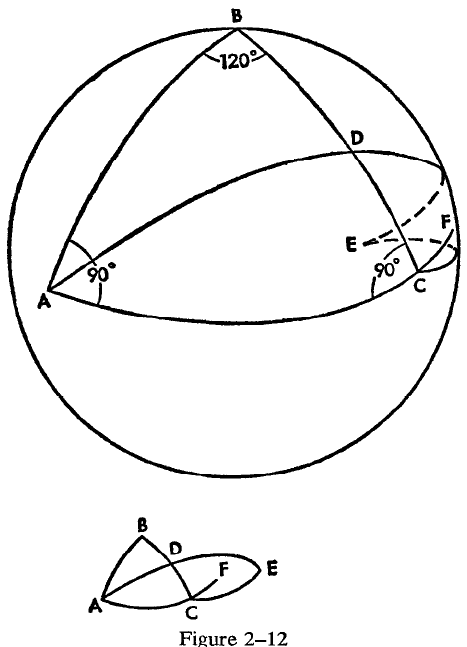
diagram. Another aid would be to draw the diagram on a truly spherical surface such as a ball.)
Looking at Figure 2-12, it is obvious why the proof of Proposition 16 or Section 19 fails. The line EC does not fall within the angle BCF but outside of it. Thus Euclid could not here conclude that angle DCF is greater than angle DCE. (In fact we know that DCF is 90° and that DCE, being equal to the angle at B, is 120°.) And Lobachevski cannot conclude that there is a limit to how large the angle ACE can become; in fact, this angle in our diagram is greater than 180°, and there is still a triangle A EC. (Angle ACE is 210° in our example.)
Now imagine that there are straight lines — not great circles — which behave like the great circles on a sphere. These would be quite different straight lines from Euclid's or Lobachevski's, of course. (Lobachevski's straight lines are also different from EucUd's; there can be an infinite number of straight lines not meeting a given line, if the lines are Lobachevski's sort, whereas there can be only one such non-meeting line if the lines are Euclid's kind.) The characteristic of this new, third sort of straight lines is that to a given line there is no non-meeting line. (All the great circles on a sphere meet twice; for example, all meridians meet at the north pole and at the south pole.) It turns out to be possible to have a geometrical system in which the straight lines in a plane are of this "quasi-spherical" sort. This new geometry is called "Riemannian" after the German mathematician Bernhard Riemann (1826-1866), who first studied it. It is, of course, different from both Euclid's geometry and Lobachevski's. For example, the sum of the angles in a Riemannian triangle is found to be greater than two right angles.
Just as the sphere provides a way of visualizing a plane geometry in which there are no parallel lines, there is another surface which enables us to visualize Lobachevski's geometry, in which there is an infinite number of parallel lines. This surface is called a "pseudosphere"; it is shown in Figure 2-13. On the pseudosphere those lines which are the shortest
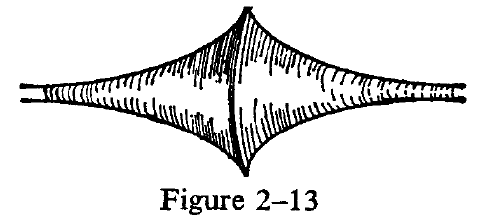
distance between two points behave like the straight lines in a Lobachevskian plane. There are many non-meeting lines to a given fine, and the sum of the angles of a triangle is less than two right angles.
Those lines on a surface which constitute the shortest distance between two points are called the "geodesies" of that surface. The straight lines in Riemannian geometry have many of the properties of the geodesies of a sphere, whereas the straight lines in Lobachevskian geometry have many of the properties of the geodesies of a pseudosphere. However, it is most important to realize that these non-Euclidean geometries are plane geometries; the sphere, the pseudosphere, and their geodesies are useful only in order to visualize these geometries. Riemannian geometry is not spherical geometry, nor is Loba-chevskian geometry pseudospherical geometry.
To sum up, there are three possibilities as regards parallel lines, each possibility giving rise to a different geometry: (1) Through a given point there is an infinite number of non-meeting lines to a given line—Lobachevskian geometry. (2) Through a given point there is one and only one non-meeting line to a given point — Euclidean geometry. (3) Through a given point there is no non-meeting line to a given line — Riemannian geometry.
Any system of geometry in which Euclid's Proposition 16 is valid eliminates the possibility of Riemannian geometry. This is the reason why, as we noted earlier, Saccheri had a certain amount of success in proving Euclid's fifth postulate. Saccheri accepted Proposition 16; consequently, he was able to demonstrate absurd conclusions from (the equivalent of) Riemann's postulate.
A system of geometry in which Euclid's Postulate 5 holds eliminates Lobachevski's hypothesis. Thus Euclid rids himself of the possibility of Riemannian geometry by means of Proposition 16, and of Lobachevskian geometry by means of Postulate 5. We should add that Proposition 16 is, in turn, based on Postulate 2 (that is, on the assumption that straight lines are infinite in length); Proposition 16 (or Lobachevski's Section 19) cannot be proved in Riemannian geometry, because in the latter straight lines are finite in length. We can now see that the proofs of Euclid's Propositions 27 and 29 are really quite similar. Both, as we have already noted, are demonstrated by use of reduction to the absurd. But the keystone to the absurdity is Proposition 16 in the first case, and Postulate 5 in the second case. Proposition 16 is the equivalent of another postulate concerning parallelism, namely, "To a given line, through a given point, there exists at least one parallel (non-meeting) line." In both Proposition 27 and Proposition 29, therefore, the absurdity is reached by the use of a postulate concerning parallel lines.
Finally, we must touch on a question that has no doubt already occurred to the reader: Which of these geometries is true? Or are any of them true? The answer is in one way simple, yet also complicated. All three geometries are in themselves equally valid. That is, each can be shown to be a consistent system. Each system contains equivalent propositions; that is, each proposition in one system has a corresponding proposition in the other systems. No one of these geometries is more true than another; this statement is not so hard to accept if we remember that geometry is not concerned with physical lines or points, but rather with ideal, mental entities. These things of the mind can, of course, be shaped by the mind (as long as no contradictions develop). If we wish, therefore, we can choose to geometrize with lines that behave like those of Riemann or those of Lobachevski rather than those of Euclid.
Yet we may also ask, which geometry applies to the things and the space around us? We are used to employing Euclidean geometry; engineers and architects certainly assume that Euclid's geometry and no other is true. Yet this is not conclusive, for it is apparent that for small figures the results which the three geometries yield would be almost indistinguishable. A small triangle on a vast sphere is very much like a plane triangle in Euclidean space. Similarly, it may be that space is Lobachevskian in character; yet it may be so large that for the small areas in human purview, the geometrical results would not be noticeably different from those of Euclidean geometry.
The question of which geometry is most suitable for physical applications is an experimental one. The German mathematician Gauss (1777-1855) performed some measurements on large triangles to determine whether the sum of their angles was 180° or not. However, his results were inconclusive; such differences from 180° as he found were so small that they might have been due to experimental error.

 MENU
MENU