FORMULAS from SOLID ANALYTIC GEOMETRY
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$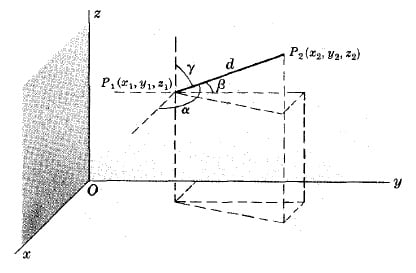
DIRECTION COSINES OF LINE JOINING POINTS $P_1(x_1,y_1,z_1)$ AND $P_2(x_2,y_2,z_2)$
$l=\cos\alpha=\frac{x_2-x_1}{d}$, $m=\cos\beta=\frac{y_2-y_1}{d}$, $n=\cos\gamma=\frac{z_2-z_1}{d}$
where $\alpha,\beta,\gamma$ are the angles which line $P_1P_2$ makes with the positive $x,y,z$ axes respectively and $d$ is given by the figure above.
RELATIONSHIP BETWEEN DIRECTION COSINES
$\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$ or $l^2+m^2+n^2=1$
DIRECTION NUMBERS
Number $L,M,N$ which are proportional to the direction cosines $l,m,n$ are called direction numbers. The relationship between them is given by
$l=\frac{L}{\sqrt{L^2+M^2+N^2}}$, $m=\frac{M}{\sqrt{L^2+M^2+N^2}}$, $n=\frac{N}{\sqrt{L^2+M^2+N^2}}$
EQUATIONS OF LINE JOINING $P_1(x_1,y_1,z_1)$ AND $P_2(x_2,y_2,z_2)$ IN STANDARD FORM
$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$ or $\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$
These are also valid if $l,m,n$ are replaced by $L,M,N$ respectively.
EQUATIONS OF LINE JOINING $P_1(x_1,y_1,z_1)$ AND $P_2(x_2,y_2,z_2)$ IN PARAMETRIC FORM
$x=x_1+lt, y=y_1+mt, z=z_1+nt$
These are also valid if $l,m,n$ are replaced by $L,M,N$ respectively.
ANGLE $\phi$ BETWEEN TWO LINES WITH DIRECTION COSINES $l_1, m_1, n_1$ AND $l_2, m_2, n_2$
$\cos\phi=l_1l_2+m_1m_2+n_1n_2$
GENERAL EQUATION OF A PLANE
$Ax+By+Cz+D=0$ [$A,B,C,D$ are constants]
EQUATION OF PLANE PASSING THROUGH POINTS $(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$
$\begin{vmatrix}x-x_1 & y-y_1 & z-z_1\\ x_2-x_1 & y_2-y_1 & z_2-z_1\\ x_3-x_1 & y_3-y_1 & z_3-z_1\end{vmatrix}=0$
or
$\begin{vmatrix} y_2-y_1 & z_2-z_1\\ y_3-y_1 & z_3-z_1\end{vmatrix}(x-x_1)$
$+\begin{vmatrix} z_2-z_1 & x_2-x_1\\ z_3-z_1 & x_3-x_1\end{vmatrix}(y-y_1)$
$+\begin{vmatrix} x_2-x_1 & y_2-y_1\\ x_3-x_1 & y_3-y_1\end{vmatrix}(z-z_1)=0$
EQUATION OF A PLANE IN INTERCEPT FORM
$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$
where $a,b,c$ are the intercepts on the $x,y,z$ axes respectively.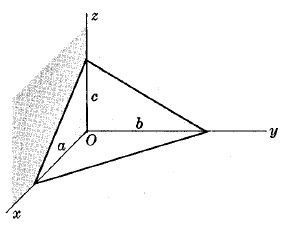
EQUATION OF LINE THROUGH $(x_0,y_0,z_0)$ AND PERPENDICULAR TO PLANE $Ax+By+Cz+D=0$
$\frac{x-x_0}{A}=\frac{y-y_0}{B}=\frac{z-z_0}{C}$ or $x=x_0+At, y=y_0+Bt, z=z_0+Ct$
Note that the direction numbers for a line perpendicular to a plane $Ax+By+Cz+D=0$ are $A,B,C$
DISTANCE FROM POINT $(x_0,y_0,z_0)$ TO A PLANE $Ax+By+Cz+D=0$.
$\frac{Ax_0+By_0+Cz_0+D}{\pm\sqrt{A^2+B^2+C^2}}$
where the sign is chosen so that the distance is nonnegative.
NORMAL FORM FOR EQUATION OF PLANE
$x\cos\alpha+y\cos\beta+z\cos\gamma=p$
where $p=$ perpendicular distance from $O$ to plane at $P$ and $\alpha, \beta, \gamma$ are angles between $OP$ and positive $x,y,z$ axes.
TRANSFORMATION OF COORDINATES INVOLVING PURE TRANSLATION
$\left\{\begin{array}{lr}x=x'+x_0\\ y=y'+y_0\\ z=z'+z_0\end{array}\right.$ or $\left\{\begin{array}{lr}x'=x-x_0\\ y'=y-y_0\\ z'=z-z_0\end{array}\right.$
where $(x, y, z)$ are old coordinates [i.e. coordinates relative to $xyz$ system],$(x', y', z')$ are new coordinates [relative to the $x'y'z'$ system] and $(x_0,y_0,z_0)$ are coordinates of the new origin $O'$ relative to the old $xyz$ coordinate system.
TRANSFORMATION OF COORDINATES INVOLVING PURE ROTATION
$\left\{\begin{array}{lr}x=l_1x'+l_2y'+l_3z'\\ y=m_1x'+m_2y'+m_3z'\\ z=n_1x'+n_2y'+n_3z'\end{array}\right.$
or
$\left\{\begin{array}{lr}x'=l_1x+m_1y+n_1z\\ y'=l_2x+m_2y+n_2z\\ z'=l_3x+m_3y+n_3z\end{array}\right.$
where the origins of the $xyz$ and $x'y'z'$ systems are the same and $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ are the direction cosines of the $x', y', z'$ axes relative to the $x, y, z$ axes respectively.
TRANSFORMATION OF COORDINATES INVOLVING TRANSLATION AND ROTATION
$\left\{\begin{array}{lr}x=l_1x'+l_2y'+l_3z'+x_0\\ y=m_1x'+m_2y'+m_3z'+y_0\\ z=n_1x'+n_2y'+n_3z'+z_0\end{array}\right.$
or
$\left\{\begin{array}{lr}x'=l_1(x-x_0)+m_1(y-y_0)+n_1(z-z_0)\\ y'=l_2(x-x_0)+m_2(y-y_0)+n_2(z-z_0)\\ z'=l_3(x-x_0)+m_3(y-y_0)+n_3(z-z_0)\end{array}\right.$
where the $O'$ of $x'y'z'$ system has coordinates $(x_0,y_0,z_0)$ relative to the $xyz$ system and $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ are the direction cosines of the $x' , y', z'$ axes relative to the $x, y, z$ axes respectively.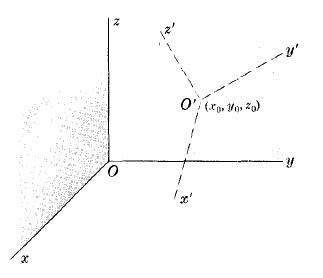
CYLINDRICAL COORDINATES $(r, \theta, z)$
A point $P$ can be located by cylindrical coordinates $(r, \theta, z)$ as well as rectangular coordinates $(x, y, z)$.
The transformation between these coordinates is
$\left\{\begin{array}{lr}x=r\cos\theta\\ y=r\sin\theta\\ z=z\end{array}\right.$ or $\left\{\begin{array}{lr}r=\sqrt{x^2+y^2}\\ \theta=\tan^{-1}\frac{y}{x}\\ z=z\end{array}\right.$ 
SPHERICAL COORDINATES $(r, \theta, \phi)$
A point $P$ can be located by spherical coordinates $(r, \theta, \phi)$ as well as rectangular coordinates $(x, y, z)$.
The transformation between those coordinates is
$\left\{\begin{array}{lr}x=r\sin\theta\cos\phi\\ y=r\sin\theta\sin\phi\\ z=r\cos\theta\end{array}\right.$
or
$\left\{\begin{array}{lr}r=\sqrt{x^2+y^2+z^2}\\ \phi=\tan^{-1}\frac{y}{x}\\ \theta=\cos^{-1}\left(\frac{z}{\sqrt{x^2+y^2+z^2}}\right)\end{array}\right.$ 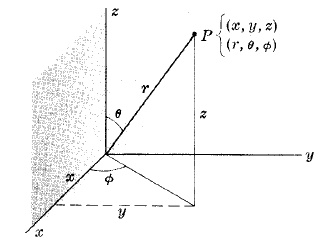
EQUATION OF A SPHERE IN RECTANGULAR COORDINATES
$(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$
where the sphere has center $(x_0,y_0,z_0)$ and radius $R$.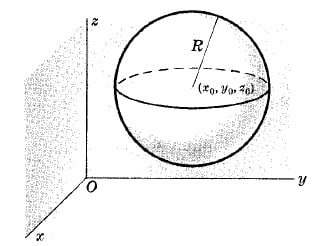
EQUATION OF SPHERE IN CYLINDRICAL COORDINATES
$r^2-2r_0r(\theta-\theta_0)+r_0^2+(z-z_0)^2=R^2$
where the sphere has center $(r_0,\theta_0,z_0)$ in cylindrical coordinates and radius $R$.
If the center is at the origin the equation is:
$r^2+z^2=R^2$
EQUATION OF SPHERE IN SPHERICAL COORDINATES
$r^2+r_0^2-2r_0 r\sin\theta\sin\theta_0\cos(\phi-\phi_0)=R^2$
where the sphere has center $(r_0,\theta_0,\phi_0)$ in spherical coordinates and radius $R$.
If the center is at the origin the equation is
$r = R$.
EQUATION OF ELLIPSOID WITH CENTER $(x_0,y_0,z_0)$ AND SEMI-AXES $a, b, c$
$\frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}+\frac{(z-z_0)^2}{c^2}=1$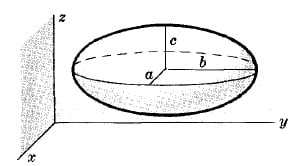
ELLIPTIC CYLINDER WITH AXIS AS z AXIS
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
where $a, b$ are semi axes of elliptic cross section.
If $b = a$ it becomes a circular cylinder of radius $a$.
ELLIPTIC CONE WITH AXIS AS z AXIS
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{z^2}{c^2}$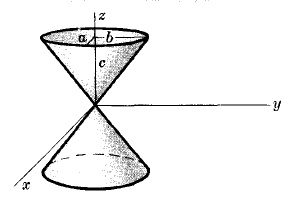
HYPERBOLOID OF ONE SHEET
$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$.
Hyperboloid - animated(the red line is straight)
HYPERBOLOID OF TWO SHEETs
$\frac{x^2}{a^2}-\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$.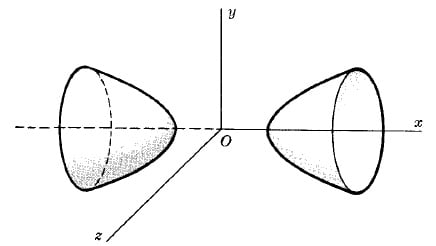
ELLIPTIC PARABOLOID
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{z}{c}$
HYPERBOLIC PARABOLOID
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=\frac{z}{c}$
Note orientation of axes in the figure.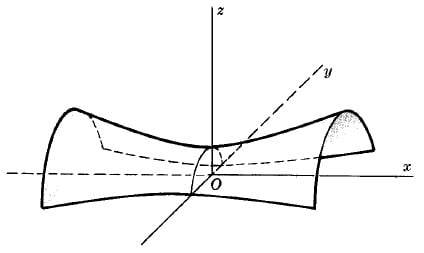

 MENU
MENU