Circle
Definition: A circle is a simple shape, consisting of those points in a plane that are a given distance from a given point - the centre.
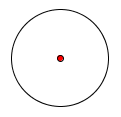
Origin: the center of a circle
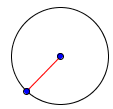
Radius: the distance from the center of a circle to any point on it.
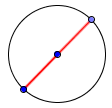
Diameter: the longest distance from one end of a circle to the other. The diameter = 2 × radius (d = 2r).
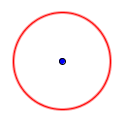
Circumference: the distance around the circle.
Circumference $= \pi \times diameter$.
Circumference $= \pi \times d = 2 \times \pi \times r$
$\pi$ - pi: a number equal to 3.141592... or $\approx \frac{22}{7}$, that is $\frac{\text{the circumference}}{\text{the diameter}}$ of any circle.
Arc: a curved line that is part of the circumference of a circle.

The arc of a circle is measured in degrees or radians - for example: 90° or $\frac{\pi}{2}$ - a quarter of the circle,
180° or $\pi$ - a half of the circle.
The arc is smaller than 360°(or $2\pi$) because that is the whole circle.
Chord: a line segment within a circle that touches 2 points on the circle.
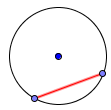
Sector: is like a slice of pie (a circle wedge).
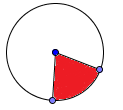
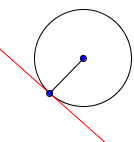
Tangent: a line perpendicular to the radius that touches ONLY one point on the circle.
Formulas
The formula for finding the circumference of a circle is $\pi \cdot \text{diameter} = 2 \cdot \pi \cdot \text{radius}$
The formula for finding the area of a circle is $\pi \cdot \text{radius}^2$
The standard notation for a radius is r, for a diameter - d, for a circumference - P and for area A.
$A = \pi \cdot r^2$
Angles
Central angle
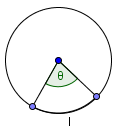
If the length of an arc is $\theta$ degrees or radians then the measurement of the central angle is also $\theta$(degrees or radians).
If you know the length of an arc(in inches, yards, foots, centimeters, meters...) you can find the measurement of its corresponding central angle($\theta$) by the formula:
$l$ is the length of the arc.
Inscribed angle
An inscribed angle is formed by two chords and vertex on the circle.
$\angle APB$ is an inscribed angle.
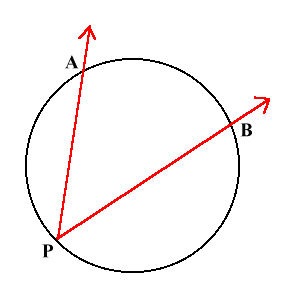
Example:
The arc $\widehat{AB}$ measures 84°.
The measurement of $\angle APB = \frac{84}{2} = 42^\circ$
Angles between two secants
Case 1: two secants intersect inside a circle.
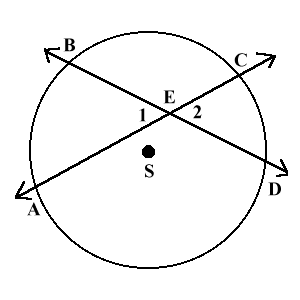
In the figure, arc AB is 60° and the arc CD is 50°.
So angle 1 and 2 measure ½(60° + 50°) = 55°
Case 2: two secants intersect outside a circle.
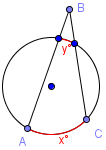
The measurement of the angle formed is equal to half the difference of the arcs.
$\angle ABC =\frac{1}{2}(x - y)$
For example: if the bigger arc measures 80° and the smaller one 30° then $\angle ABC = \frac{1}{2}(80 - 30) = \frac{1}{2} \cdot 50 = 25^\circ$
Formula for intersecting chords
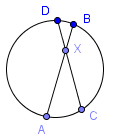
When two chords intersect inside a circle then:
Area of sector
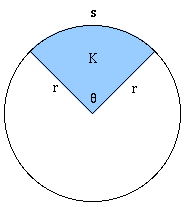
$\theta$ is the measurement of the central angle.
If the angle θ is in degrees, then the area = $\frac{\theta}{360} \pi r^2$
If the angle θ is in radians, then the area = $\frac{\theta}{2} r^2$
Area of a Circular Ring
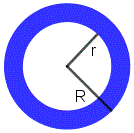
Area = $\pi$(R2 - r2)
Area of a Circular Trapezoid

Area = $\pi(R^2 - r^2)\frac{\theta}{360}$

 MENU
MENU