 Регистрирайте се Регистрирайте се
| Предишната тема :: Следващата тема |
| Автор |
Съобщение |
estoyanovvd
Фен на форума

Регистриран на: 19 Sep 2006
Мнения: 764
Местожителство: Видин
   
гласове: 67
|
 Пуснато на: Wed Mar 11, 2009 9:03 am Заглавие: Геометрично неравенство Пуснато на: Wed Mar 11, 2009 9:03 am Заглавие: Геометрично неравенство |
|
|
| Нека точка М е вътрешна за равностранен триъгълник АВС със страна 1. Докажете, че от отсечките МА, МВ и МС има две, чието произведение не надминава [tex]\frac{1}{ 3} [/tex] и две, чието произведение е по-голямо или равно на [tex]\frac{1}{ 3} [/tex].
|
|
| Върнете се в началото |
|
 |
Реклама
|
 Пуснато на: Заглавие: Реклама Пуснато на: Заглавие: Реклама |
|
|
|
|
|
| Върнете се в началото |
|
 |
estoyanovvd
Фен на форума

Регистриран на: 19 Sep 2006
Мнения: 764
Местожителство: Видин
   
гласове: 67
|
 Пуснато на: Mon Mar 23, 2009 10:05 am Заглавие: Пуснато на: Mon Mar 23, 2009 10:05 am Заглавие: |
|
|
Някой може ли да реши тази задача? 
|
|
| Върнете се в началото |
|
 |
luboslav_p
Начинаещ
Регистриран на: 16 Feb 2008
Мнения: 33
Местожителство: София
  
гласове: 7
|
 Пуснато на: Mon Mar 23, 2009 10:59 am Заглавие: Пуснато на: Mon Mar 23, 2009 10:59 am Заглавие: |
|
|
Нека точката M е дадена и CM≥BM≥AM. Ще докажем, че произведението на някои две отсечки е не повече от 1/3. Да фиксираме разстоянието BM=a т.е. M лежи на окръжност k с център B и радиус a. Нека k пресича AB и BC в точки P и Q съответно. Не е трудно да се види, че движейки се по дъгата PQ в посока от P към Q, дължината на AM се увеличава, а тази на CM намалява. Това е така, защото в триъгълник ABM AB и BM са с фиксирани дължини и с движението на M ъгъл ABM расте т.е. намалява cos на ъгъла т.е. AM расте. Аналогично CM намалява. Нека V е средата на дъгата PQ. Очевидно AV=CV. Тъй като CM≥AM, то M е от дъгата PV. Сега запозваме да движим M към V по дъгата. Да отбележим, че AM.BM е минималното произведение, а с движението на M AM расте, а BM остава същата. Така може да увеличаваме произведението докато някои две от трите отсечки станат равни( а това ще се случи със сигурност). Достигнахме до нова конфигурация с не по-малко произведение на двете най-малки отсечки, за което някои две от тях са равни. Без ограничение AM=BM и центърът на триъгълника е O. Това значи, че C,M и O са на една права.
1сл) Ако O е между M и C, то AM=BM≤AO=BO т.е. AM.BM≤AO.BO=1/3.
2сл) Ако M е между O и C, то AM≤AO+OM и оттук AM+CM≤AO+OM+CM=AO+CO. Сега AM.CM≤((AM+CM)/2)2≤((AO+OC)/2)2=AO2=1/3.
Аналогично се доказва, че произведението на двете най-големи отсечки е поне 1/3.
|
|
| Върнете се в началото |
|
 |
estoyanovvd
Фен на форума

Регистриран на: 19 Sep 2006
Мнения: 764
Местожителство: Видин
   
гласове: 67
|
 Пуснато на: Mon Mar 23, 2009 12:00 pm Заглавие: Пуснато на: Mon Mar 23, 2009 12:00 pm Заглавие: |
|
|
Изглежда ми вярно за по-малко или равно на една трета. Би ли написал аналогичното за по-голямо или равно на една трета?
Задачата има много по-лесно решение. Но ще почакам още някой да се пробва!!!
|
|
| Върнете се в началото |
|
 |
zhivko_sh
Начинаещ
Регистриран на: 22 Feb 2008
Мнения: 37
   
гласове: 12
|
 Пуснато на: Mon Mar 23, 2009 3:40 pm Заглавие: Пуснато на: Mon Mar 23, 2009 3:40 pm Заглавие: |
|
|
| Нарочно не исках да пиша веднага решение на тази задача, но след като така или иначе Любо вече написа решение ще дам моето. Ще докажем, че ако имаме равностранен триъгълник със страна [tex]a[/tex], то някое от произведенията е не по-голямо от [tex]\frac{a^2}{3 } [/tex], а някое е не по-малко от [tex]\frac{a^2}{3 } [/tex]. Нека O е центърът на описаната около ABC окръжност. Тогава БОО М попада в триъгълник ОAB (включително по контура). От една твърде известна задача от 7 клас следва, че [tex]MA+MB\le OA+OB[/tex](за тези, които са забравили как става това, достатъчно е да се разгледа пресечната точка на AM и OB и правим 2 пъти неравенство на триъгълника). Тогава [tex]MA+MB\le OA+OB=2R[/tex], където R е радиусът на описаната около ABC окръжност. Тогава имаме [tex]MA.MB\le \frac{(MA+MB)^2}{ 4}\le \frac{(2R)^{2}}{4 }=R^{2} [/tex]. Сега остава да отбележим, че от синусова теорема [tex]R=\frac{a}{\sqrt{3} } [/tex] и значи [tex]MA.MB\le \frac{a^2}{3 } [/tex]. При a=1 се получава конкретната задача. За [tex]\ge [/tex] задачата е почти тривиална.(имаме [tex]S=\frac{a^{2}\sqrt{3} }{4 } [/tex], а ако и трите произведения са [tex]<\frac{a^{2}}{3 } [/tex], то като означим трите ъгъла при М с [tex]\alpha ,\beta,\gamma [/tex] и използваме [tex]sin\alpha +sin\beta +sin\gamma \le \frac{3\sqrt{3} }{ 2} [/tex] всичко веднага излиза - сумата на трите лица става по-малко от [tex]S=\frac{a^{2}\sqrt{3} }{4 } [/tex]).
|
|
| Върнете се в началото |
|
 |
estoyanovvd
Фен на форума

Регистриран на: 19 Sep 2006
Мнения: 764
Местожителство: Видин
   
гласове: 67
|
 Пуснато на: Mon Mar 23, 2009 7:53 pm Заглавие: Пуснато на: Mon Mar 23, 2009 7:53 pm Заглавие: |
|
|
| zhivko_sh написа: | | Нарочно не исках да пиша веднага решение на тази задача, но след като така или иначе Любо вече написа решение ще дам моето. Ще докажем, че ако имаме равностранен триъгълник със страна [tex]a[/tex], то някое от произведенията е не по-голямо от [tex]\frac{a^2}{3 } [/tex], а някое е не по-малко от [tex]\frac{a^2}{3 } [/tex]. Нека O е центърът на описаната около ABC окръжност. Тогава БОО М попада в триъгълник ОAB (включително по контура). От една твърде известна задача от 7 клас следва, че [tex]MA+MB\le OA+OB[/tex](за тези, които са забравили как става това, достатъчно е да се разгледа пресечната точка на AM и OB и правим 2 пъти неравенство на триъгълника). Тогава [tex]MA+MB\le OA+OB=2R[/tex], където R е радиусът на описаната около ABC окръжност. Тогава имаме [tex]MA.MB\le \frac{(MA+MB)^2}{ 4}\le \frac{(2R)^{2}}{4 }=R^{2} [/tex]. Сега остава да отбележим, че от синусова теорема [tex]R=\frac{a}{\sqrt{3} } [/tex] и значи [tex]MA.MB\le \frac{a^2}{3 } [/tex]. При a=1 се получава конкретната задача. За [tex]\ge [/tex] задачата е почти тривиална.(имаме [tex]S=\frac{a^{2}\sqrt{3} }{4 } [/tex], а ако и трите произведения са [tex]<\frac{a^{2}}{3 } [/tex], то като означим трите ъгъла при М с [tex]\alpha ,\beta,\gamma [/tex] и използваме [tex]sin\alpha +sin\beta +sin\gamma \le \frac{3\sqrt{3} }{ 2} [/tex] всичко веднага излиза - сумата на трите лица става по-малко от [tex]S=\frac{a^{2}\sqrt{3} }{4 } [/tex]). |
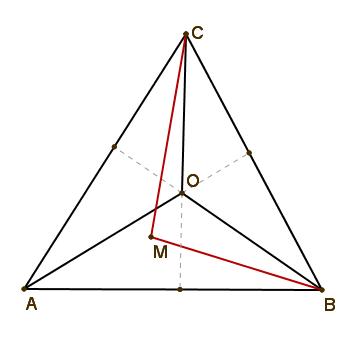
Абсолютно точно и почти като моето решение с изключение на това, че радиусът се намира с Питагоровата теорема, а за по-голямо или равно е още по-просто от приложения чертеж, който не е трудно да се види, че винаги се случва!!!(Имам впредвид, че О е вътрешна за триъгълника ВСМ)
| Description: |
|
| Големина на файла: |
11.17 KB |
| Видяна: |
1170 пъти(s) |
|
|
|
| Върнете се в началото |
|
 |
estoyanovvd
Фен на форума

Регистриран на: 19 Sep 2006
Мнения: 764
Местожителство: Видин
   
гласове: 67
|
 Пуснато на: Mon Mar 23, 2009 7:56 pm Заглавие: Пуснато на: Mon Mar 23, 2009 7:56 pm Заглавие: |
|
|
Сега искам да ви попитам ще се сетите ли от къде ми хрумна идеята за тази задачка?  Който се сети, ще бъде възнаграден!!! Който се сети, ще бъде възнаграден!!!
|
|
| Върнете се в началото |
|
 |
ferry2
Напреднал

Регистриран на: 10 Dec 2007
Мнения: 442
Местожителство: гр.Пловдив
  
гласове: 24
|
 Пуснато на: Mon Mar 23, 2009 8:36 pm Заглавие: Пуснато на: Mon Mar 23, 2009 8:36 pm Заглавие: |
|
|
| estoyanovvd написа: | Сега искам да ви попитам ще се сетите ли от къде ми хрумна идеята за тази задачка?  Който се сети, ще бъде възнаграден!!! Който се сети, ще бъде възнаграден!!! |
Вашата задача доста прилича на 2з от ІІ-ри кръг на Турнира на Декана на ФМИ!
|
|
| Върнете се в началото |
|
 |
estoyanovvd
Фен на форума

Регистриран на: 19 Sep 2006
Мнения: 764
Местожителство: Видин
   
гласове: 67
|
 Пуснато на: Mon Mar 23, 2009 9:33 pm Заглавие: Пуснато на: Mon Mar 23, 2009 9:33 pm Заглавие: |
|
|
Нееее, не е това!
Прилича на задача от конкурс!!! Но не е този!!!   
|
|
| Върнете се в началото |
|
 |
|
|
Не Можете да пускате нови теми
Не Можете да отговаряте на темите
Не Можете да променяте съобщенията си
Не Можете да изтривате съобщенията си
Не Можете да гласувате в анкети
Може да прикачвате файлове
Може да сваляте файлове от този форум
|
|