 Регистрирайте се Регистрирайте се
| Предишната тема :: Следващата тема |
| Автор |
Съобщение |
ганка симеонова
SUPER VIP

Регистриран на: 10 Jan 2008
Мнения: 5985
Местожителство: софия
    
гласове: 298
|
 Пуснато на: Mon Mar 09, 2009 2:07 pm Заглавие: Примерна - УАСГ Пуснато на: Mon Mar 09, 2009 2:07 pm Заглавие: Примерна - УАСГ |
|
|
Дадена е правилна четириъгълна пирамида ABCDM с основа ABCD. Нека [tex]AB=a, AM=ka[/tex], където к е параметър.
а) Равнина минава през точка А и е перпендикулярна на правата МС. При каква стойност на к сечението на пирамидата с равнината е четириъгълник?
б) Нека [tex]k=\sqrt{2} [/tex]. Докажете, че в сечението от а) може да се впише окръжност и намерете нейния радиус.
в) Нека точка Р е среда на СМ и точка Q е срада на АМ. Намерете косинусът на ъгъла между правите ВР и QD.
|
|
| Върнете се в началото |
|
 |
Реклама
|
 Пуснато на: Заглавие: Реклама Пуснато на: Заглавие: Реклама |
|
|
|
|
|
| Върнете се в началото |
|
 |
_sssss
Фен на форума
Регистриран на: 07 Dec 2008
Мнения: 633
   
гласове: 50
|
 Пуснато на: Mon Mar 09, 2009 3:42 pm Заглавие: Пуснато на: Mon Mar 09, 2009 3:42 pm Заглавие: |
|
|
Сечението не е ли винаги четириъгълник? (когато съществува)* Значи AMC < 90° <=> 0< sinAMC <1; 0< cosAMC <1
k>1
*Поне пирамидата от хлебна гума и клечки за зъби твърди така.  Някой ще ми каже ли програма за чертане на обемни фигури? Някой ще ми каже ли програма за чертане на обемни фигури? 
|
|
| Върнете се в началото |
|
 |
Spider Iovkov
VIP

Регистриран на: 12 Jan 2007
Мнения: 1273
   
гласове: 129
|
 Пуснато на: Fri Mar 13, 2009 8:24 pm Заглавие: Пуснато на: Fri Mar 13, 2009 8:24 pm Заглавие: |
|
|
Ще използваме един факт, произтичащ от това, че ако две равнини са перпедикулярни, то всяка права от едната равнина е перпендикулярна на коя да е права от другата. В конкретната задача трябва да се прекара такава равнина през върха [tex]A[/tex] на пирамидата, че равнината да е перпендикулярна на околния ръб [tex]MC[/tex]. Построяваме [tex]AO\bot MC, O\in MC[/tex]. След това от точката [tex]O[/tex] издигаме перпендикуляри, пресичащи околните ръбове [tex]MB[/tex] и [tex]MD[/tex] съответно в точките [tex]N[/tex] и [tex]L[/tex]: [tex]NO\bot MC, LO\bot MC[/tex]. Свързваме последователно [tex]A, N, O, L[/tex] и получаваме исканото сечение.
Да означим [tex]\angle AMC=\varphi[/tex]. Тогава от косинусовата теорема за [tex]\triangle AMC \Rightarrow AC^2=AM^2+CM^2-2.AM.CM. cos \varphi \Leftrightarrow 2a^2=(ak)^2+(ak)^2-2.ak.ak. cos\varphi \Leftrightarrow k^2-k^2 cos\varphi=1 \Leftrightarrow cos\varphi=\frac{k^2-1}{k^2}[/tex]. Сега, за да е сечението на равнината с пирамидата четириъгълник, то трябва [tex]cos\varphi<90^\circ \Leftrightarrow cos\varphi>0 \Leftrightarrow \frac{k^2-1}{k^2}>0 \Leftrightarrow k^2-1>0 \Leftrightarrow k\in (-\infty;-1)\cup (1;+\infty)[/tex]. Но тъй като от този параметър зависи дължината на отсечка, то [tex]k\in (1;+\infty)[/tex]. При [tex]\varphi=90^\circ[/tex] сечението с равнината съвпада със сечението на пирамидата по диагонала [tex]AC[/tex] от основата.
Сега, понеже [tex]AC=a\sqrt{2}[/tex] (следва от [tex]\triangle ABC[/tex]) и [tex]AM=ka=a\sqrt{2}[/tex], то [tex]AC=AM[/tex], от което получаваме, че точката [tex]O[/tex] разполовява околния ръб [tex]CM[/tex], или [tex]\fbox {CO=MO=\frac{a\sqrt{2}}{2}}[/tex]. Пресмятаме също [tex]AO^2+CO^2=AC^2 \Leftrightarrow AO^2+(\frac{a\sqrt{2}}{2})^2=2a^2 \Leftrightarrow \fbox {AO=\frac{a\sqrt{6}}{2}}[/tex].
[tex]NO\bot BM, MO=CO \Rightarrow MN=CN; \triangle ABN \simeq \triangle CBN \Rightarrow^{I \cyr pr.} \fbox {AN=CN=\frac{2a\sqrt{2}}{3}}[/tex]
Понеже пирамидата е правилна, то ще е изпълнено [tex]\angle AMB=\angle BMC=\angle CMD=\angle AMD=\varphi[/tex]. От косинусовата теорема за [tex]\triangle BCM \Rightarrow BC^2=BM^2+CM^2-2.BM.CM. cos\varphi \Leftrightarrow a^2=(a\sqrt{2})^2+(a\sqrt{2})^2-2.a\sqrt{2}.a\sqrt{2}.cos\varphi \Leftrightarrow \fbox {cos\varphi=\frac{3}{4}} \Rightarrow \fbox {sin\varphi=\frac{\sqrt{7}}{4}}[/tex].
Разглеждаме [tex]\triangle MON[/tex]. От него имаме [tex]cos\angle NMO=cos\varphi=\frac{MO}{MN} \Leftrightarrow \frac{MO}{MN}=\frac{3}{4} \Leftrightarrow \frac{a\sqrt{2}}{\cancel 2MN}=\frac{3}{\cancel 2.2} \Leftrightarrow \fbox {MN=\frac{2a\sqrt{2}}{3}}[/tex].
От същия триъгълник определяме [tex]sin\varphi=\frac{NO}{MN} \Leftrightarrow \frac{NO}{MN}=\frac{\sqrt{7}}{4} \Leftrightarrow \frac{3NO}{\cancel 2a\sqrt{2}}=\frac{\sqrt{7}}{\cancel 2.2} \Leftrightarrow \fbox {NO=\frac{a\sqrt{14}}{6}}[/tex].
Нека [tex]MH[/tex] е височината на пирамидата, [tex]H\in (ABCD)[/tex], и [tex]ANOL[/tex] има ортогонална проекция върху основата съответно [tex]AN'O'L'[/tex]. Тогава [tex]BN'=DL', L'N'=LN[/tex] (защото [tex]DBNL[/tex] е равнобедрен трапец). Имаме [tex]MH=a\sqrt{\frac{3}{2}}[/tex]. От [tex]\triangle BHM \Rightarrow sin\angle HBM=\frac{MH}{BM}=\frac{\cancel a\sqrt{3}}{\sqrt{2}}.\frac{1}{\cancel a\sqrt{2}} \Leftrightarrow sin \angle HBM=\frac{\sqrt{3}}{2} \Leftrightarrow \angle HBM=60^\circ \Rightarrow \angle HCM=\angle HDM=\angle HAM=60^\circ[/tex] (равни ъгли между околните ръбове и основата на пирамидата). Тогава [tex]\angle BNN'=30^\circ \Leftrightarrow BN'=\frac{BN}{2} \Leftrightarrow BN'=\frac{a\sqrt{2}}{3.2} \Leftrightarrow \fbox {BN'=\frac{a\sqrt{2}}{6}}[/tex] (катет срещу ъгъл от трийсет градуса в правоъгълния [tex]\triangle BNN'[/tex]). По същата аналогия можем да запишем [tex]\angle COO'=30^\circ \Leftrightarrow CO'=\frac{CO}{2} \Leftrightarrow CO'=\frac{a\sqrt{2}}{2.2} \Leftrightarrow \fbox {CO'=\frac{a\sqrt{2}}{4}}[/tex].
Но [tex]AO'+CO'=AC \Rightarrow \fbox {AO'=\frac{3a\sqrt{2}}{4}}[/tex]. Ясно е и че [tex]\fbox {L'N'=\frac{2a\sqrt{2}}{3}}[/tex]; идва от [tex]DL'+L'N'+N'B=BD \Leftrightarrow L'N'=BD-2BN'=BD-2DL'[/tex].
От [tex]\triangle AO'O \Rightarrow cos\angle OAO'=\frac{AO'}{AO} \Leftrightarrow cos\angle OAO'=\frac{3a\sqrt{2}}{4}.\frac{2}{a\sqrt{6}} \Leftrightarrow cos\angle OAO'=\frac{\sqrt{3}}{2} \Leftrightarrow \fbox {\angle OAO'=30^\circ}[/tex].
Сега пресмятаме лицето на проекцията [tex]AN'O'L'[/tex]: [tex]S_{AN'O'L'}=\frac{L'N'.AO'}{2}[/tex] (защото ъгълът между диагоналите на четириъгълника е прав) [tex]\Leftrightarrow \fbox {S_{AN'O'L'}=\frac{a^2}{2}}[/tex].
От друга страна, за всеки многоъгълник, който се проектира върх равнина, е в сила равенството [tex]S'=S cos\gamma[/tex], където [tex]S'[/tex] е лицето на проекцията на многоъгълника върху равнината, [tex]S[/tex] е лицето на многоъгълника, а [tex]\gamma[/tex] е ъгълът между равнините, в които са многоъгълникът и проекцията му. В такъв случай получаваме
[tex]S_{AN'O'L'}=S_{ANOL} cos 30^\circ \Leftrightarrow S_{ANOL}=\frac{S_{AN'O'L'}}{cos 30^\circ} \Leftrightarrow \fbox {S_{ANOL}=\frac{a^2\sqrt{3}}{3}}[/tex].
Но [tex]ANOL[/tex] е вписан в окръжност и тогава [tex]AN+OL=NO+AL=p[/tex]. Тогава [tex]S_{ANOL}=pr \Leftrightarrow r=\frac{S_{ANOL}}{p} \Leftrightarrow r=\frac{a^2\sqrt{3}}{3}.\frac{6}{a\sqrt{14}+4a\sqrt{2}} \Leftrightarrow r=\frac{a\sqrt{6}(4-\sqrt{7})}{9}[/tex] (след рационализация на знаменателя).
|
|
| Върнете се в началото |
|
 |
_sssss
Фен на форума
Регистриран на: 07 Dec 2008
Мнения: 633
   
гласове: 50
|
|
| Върнете се в началото |
|
 |
ганка симеонова
SUPER VIP

Регистриран на: 10 Jan 2008
Мнения: 5985
Местожителство: софия
    
гласове: 298
|
 Пуснато на: Mon Mar 16, 2009 8:12 am Заглавие: Пуснато на: Mon Mar 16, 2009 8:12 am Заглавие: |
|
|
| И аз имам съмнения. Тези прави не са успоредни на дадените.
|
|
| Върнете се в началото |
|
 |
inimitably
Редовен
Регистриран на: 13 Nov 2008
Мнения: 102
     
гласове: 25
|
 Пуснато на: Wed Mar 18, 2009 3:11 pm Заглавие: Пуснато на: Wed Mar 18, 2009 3:11 pm Заглавие: |
|
|
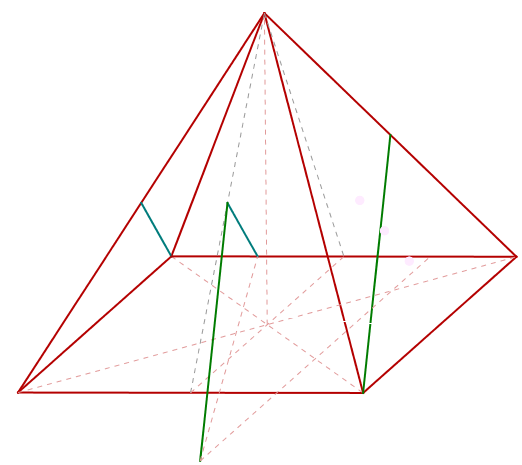
Мисля си , че е това 
| Description: |
|
| Големина на файла: |
30.95 KB |
| Видяна: |
1796 пъти(s) |
|
|
|
| Върнете се в началото |
|
 |
r2d2
VIP

Регистриран на: 28 Feb 2007
Мнения: 1936
Местожителство: in the galaxy (Far Far Away)
   
гласове: 179
|
 Пуснато на: Wed Mar 18, 2009 3:16 pm Заглавие: Пуснато на: Wed Mar 18, 2009 3:16 pm Заглавие: |
|
|
| Емо написа: | | Ще използваме един факт, произтичащ от това, че ако две равнини са перпедикулярни, то всяка права от едната равнина е перпендикулярна на коя да е права от другата. |
Емо, това е безумие!
|
|
| Върнете се в началото |
|
 |
NoThanks
Гост
|
 Пуснато на: Wed Mar 18, 2009 8:36 pm Заглавие: Пуснато на: Wed Mar 18, 2009 8:36 pm Заглавие: |
|
|
Ъгълът се намира най-лесно с вектори. Въвеждаме базис с начало т.А и означаваме:
[tex]\vec{AB}=\vec{a} \; \vec{AD}=\vec{b} \; \vec{AM}=\vec{c}[/tex] Непосредствено се изразяват [tex]\vec{QD}=\vec{b} - \vec{\frac{c}{2}} \; \vec{BP}=\frac{1}{2}(\vec{c}-\vec{a}+\vec{b})[/tex] От друга страна имаме и [tex]\vec{a}.\vec{c}=\frac{a^2}{2} \; \vec{b}.\vec{c}=\frac{a^2}{2} \; \vec{a}.\vec{b}=0[/tex](тук трябва да приложим и 1 косинусова теорема в някоя от околните стени за да намерим скаларното произведение). Сега за [tex]\vec{DQ}.\vec{BP}=\frac{a^2(3-k^2)}{4}=\frac{a^2(2+k^2)cos\varphi}{2} \Rightarrow cos\varphi = \frac{3-k^2}{2(2+k^2)}[/tex] където фи е търсеният ъгъл.
|
|
| Върнете се в началото |
|
 |
|
|
Не Можете да пускате нови теми
Не Можете да отговаряте на темите
Не Можете да променяте съобщенията си
Не Можете да изтривате съобщенията си
Не Можете да гласувате в анкети
Може да прикачвате файлове
Може да сваляте файлове от този форум
|
|