 Регистрирайте се Регистрирайте се
Да се намерят острите ъгли на триъгълника
|
| Предишната тема :: Следващата тема |
| Автор |
Съобщение |
baroveca
Напреднал

Регистриран на: 26 Feb 2009
Мнения: 347
   
гласове: 14
|
 Пуснато на: Tue Dec 29, 2009 1:11 pm Заглавие: Да се намерят острите ъгли на триъгълника Пуснато на: Tue Dec 29, 2009 1:11 pm Заглавие: Да се намерят острите ъгли на триъгълника |
|
|
| В острите ъгли на правоъгълен триъгълник са вписани два равни допиращи се един до друг два кръга.Сумата от лицата на тези кръгове и равна на лицето на кръга,вписан в триъгълника.Намерете острите ъгли на триъгълника.
|
|
| Върнете се в началото |
|
 |
Реклама
|
 Пуснато на: Заглавие: Реклама Пуснато на: Заглавие: Реклама |
|
|
|
|
|
| Върнете се в началото |
|
 |
martin123456
Фен на форума

Регистриран на: 23 Oct 2009
Мнения: 533
    
гласове: 15
|
 Пуснато на: Tue Dec 29, 2009 2:08 pm Заглавие: Re: Да се намерят острите ъгли на триъгълника Пуснато на: Tue Dec 29, 2009 2:08 pm Заглавие: Re: Да се намерят острите ъгли на триъгълника |
|
|
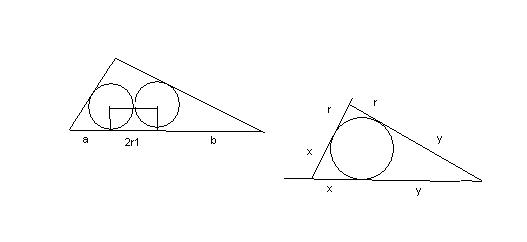
[tex](r+x)^2+(r+y)^2=(x+y)^2[/tex]
центъра на едната малка окръжност минава през ъглопол на ъгъл A, както и този на вписаната окр в ABC. значи [tex]tg\frac{\alpha}{2}=\frac{r}{x}=\frac{a}{r_1}[/tex]=>[tex]a=\frac{rr_1}{x}[/tex]. аналогично [tex]y=\frac{rr_1}{y}[/tex].
от даденото равенство с лицата: [tex]r=\sqrt{2}r_1[/tex].
[tex]AB=(x+y)^2=a+b+2r_1[/tex]
заместваме и трябва да стане
| Description: |
|
| Големина на файла: |
8.56 KB |
| Видяна: |
2866 пъти(s) |
|
|
|
| Върнете се в началото |
|
 |
Spider Iovkov
VIP

Регистриран на: 12 Jan 2007
Мнения: 1273
   
гласове: 129
|
 Пуснато на: Tue Dec 29, 2009 2:09 pm Заглавие: Пуснато на: Tue Dec 29, 2009 2:09 pm Заглавие: |
|
|
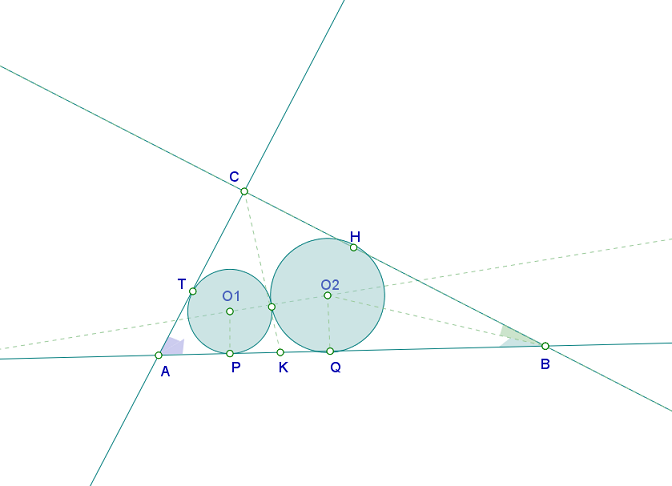
Нека означенията са както на картинката и нека [tex]\angle BAC=\alpha, \, O_{1}P=r_{1}, \, O_{2}Q=r_{2}[/tex], [tex]r[/tex] е радиусът на вписаната в [tex]\triangle ABC[/tex] окръжност. Понеже окръжностите са еднакви, то лицата им са равни, т. е.
[tex]S_{k_{1}}=S_{k_{2}} \Leftrightarrow \pi r_{1}^2 = \pi r_{2}^2 \Leftrightarrow r_{1}^2=r_{2}^2 \Leftrightarrow r_{1}=r_{2}[/tex].
По условие
[tex]S_{k_{1}}+S_{k_{2}}=S_{k} \Leftrightarrow 2S_{k_{1}}=S_{k} \Leftrightarrow 2 \pi r_{1}^2 = \pi r^2 \Leftrightarrow 2r_{1}^2=r^2 \Leftrightarrow r=r_{1}\sqrt{2}[/tex].
Сега, от [tex]O_{1}PQO_{2}[/tex] − правоъгълник, получаваме [tex]O_{1}O_{1} || AB[/tex]. Но [tex]CK[/tex] е допирателна в една и съща точка към двете окръжности, откъдето [tex]O_{1}O_{2} \bot CK \Leftrightarrow AB \bot CK[/tex] − или [tex]CK[/tex] е височина към хипотенузата в правоъгълния [tex]\triangle ABC[/tex]. Усещаме се, че
[tex]\triangle ACK \sim \triangle ABC \Rightarrow \frac{AC}{AB}=\frac{CK}{BC}=\frac{AK}{AC}=\frac{r_{1}}{r} = cos \alpha[/tex].
Обаче [tex]\frac{r_{1}}{r} = cos\alpha \Leftrightarrow \frac{r_{1}}{r_{1}\sqrt{2}} = cos\alpha \Leftrightarrow cos\alpha = \frac{\sqrt{2}}{2} \Leftrightarrow cos\alpha = cos 45^\circ \Leftrightarrow \alpha = 45^\circ \Leftrightarrow \beta=45^\circ[/tex].
| Description: |
|
| Големина на файла: |
36.8 KB |
| Видяна: |
2808 пъти(s) |
|
|
|
| Върнете се в началото |
|
 |
ганка симеонова
SUPER VIP

Регистриран на: 10 Jan 2008
Мнения: 5985
Местожителство: софия
    
гласове: 298
|
 Пуснато на: Tue Dec 29, 2009 2:11 pm Заглавие: Пуснато на: Tue Dec 29, 2009 2:11 pm Заглавие: |
|
|
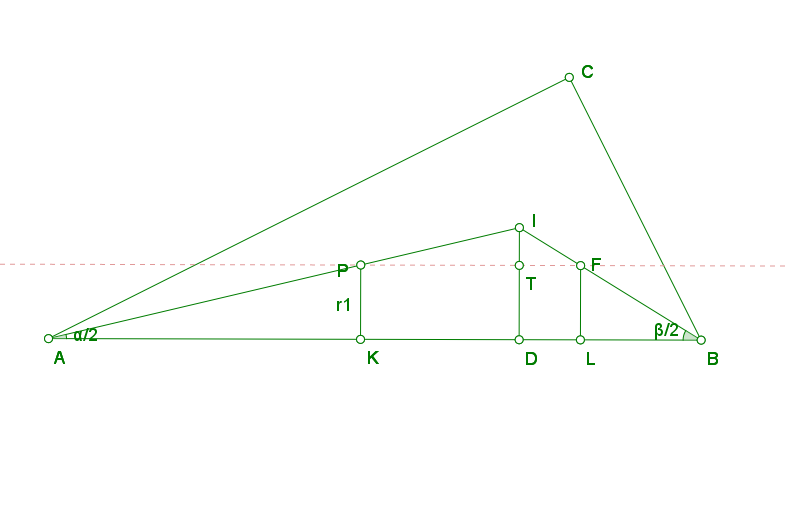
Нека Р и F са цемтровете на двата еднакви кръга, с радиуси [tex]r_1[/tex], a I- на кръга, вписан в триъгълника с радиус [tex]r[/tex]
От условието за равнолицевост=> [tex]r=\sqrt{2} r_1[/tex]
Тогава:
[tex]PF=2r_1; ID=r; IT=r-r_1; AB=c[/tex]
От подобните [tex]\Delta PFI; \Delta ABI=>\frac{2r_1}{c } =\frac{r-r_1}{ r} =>\frac{r}{c } =\frac{\sqrt{2}-1 }{ 2} [/tex]
Но, [tex]r=\frac{a+b-c}{2 } =>\frac{a+b-c}{ c} =\sqrt{2} -1=>sin\alpha +cos\alpha -1=\sqrt{2} -1=>sin\alpha +cos\alpha =\sqrt{2} [/tex]. Полученото е най- голяма стойност за сбора и се достига при [tex]sin\alpha =cos\alpha =\frac{\sqrt{2} }{2 } =>\alpha =45^\circ [/tex]
| Description: |
|
| Големина на файла: |
19.91 KB |
| Видяна: |
2858 пъти(s) |
|
|
|
| Върнете се в началото |
|
 |
|
|
Не Можете да пускате нови теми
Не Можете да отговаряте на темите
Не Можете да променяте съобщенията си
Не Можете да изтривате съобщенията си
Не Можете да гласувате в анкети
Може да прикачвате файлове
Може да сваляте файлове от този форум
|
|