 Регистрирайте се Регистрирайте се
| Предишната тема :: Следващата тема |
| Автор |
Съобщение |
stefan_vn
Начинаещ
Регистриран на: 07 Dec 2009
Мнения: 3
 
|
 Пуснато на: Mon Dec 07, 2009 8:36 pm Заглавие: Затруднение със задача ! Пуснато на: Mon Dec 07, 2009 8:36 pm Заглавие: Затруднение със задача ! |
|
|
Затрудних се с една задача ако нямой може да ми помогне ...
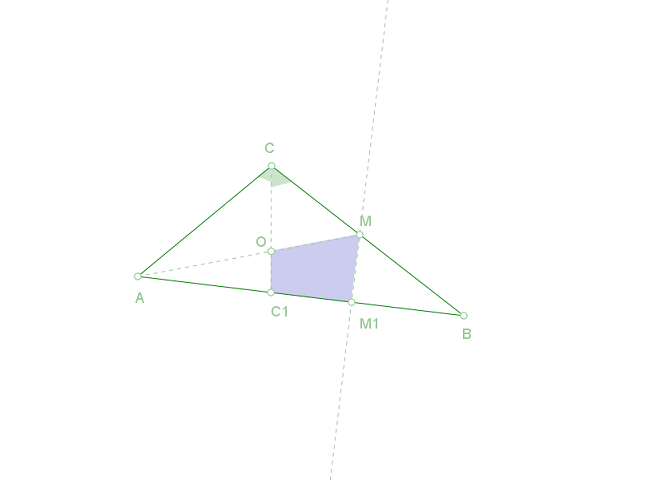
Даден е разнострания тъпоъгълен трийгълник ▲А B C .... C >90
Прекарана е Медианата АМ към страната BC
Ъглополовящата на ъгъл C пресича медианата на страната BC в т. O и АB в т.C1
Oт т.М е пуснат перпендиколяр към AB - MM1
Да се намери лицето на четериъгълника ОC1M1M
Ако ъгъл А=alpha
ъгъл B=β
BC=2a.
OC=7/5a
MM1=3/5а
|
|
| Върнете се в началото |
|
 |
Реклама
|
 Пуснато на: Заглавие: Реклама Пуснато на: Заглавие: Реклама |
|
|
|
|
|
| Върнете се в началото |
|
 |
Spider Iovkov
VIP

Регистриран на: 12 Jan 2007
Мнения: 1273
   
гласове: 129
|
 Пуснато на: Tue Dec 08, 2009 12:17 pm Заглавие: Пуснато на: Tue Dec 08, 2009 12:17 pm Заглавие: |
|
|
По правилото за сбор на ъглите в триъгълника намираме [tex]\angle ACB=180^\circ-(\alpha+\beta)[/tex], откъдето [tex]\angle ACC_{1}=\angle BCC_{1}=90^\circ-\frac{\alpha+\beta}{2}[/tex]. Тогава [tex]\angle AC_{1}C=90^\circ+\frac{\beta-\alpha}{2} \Leftrightarrow \angle BC_{1}C=90^\circ-\frac{\beta-\alpha}{2}[/tex]. Имаме [tex]S_{\triangle BCC_{1}}=S_{\triangle COM}+S_{\triangle BMM_{1}}+S_{OC_{1}M_{1}M} \Leftrightarrow S_{OC_{1}M_{1}M}=S_{\triangle BCC_{1}}-S_{\triangle COM}-S_{\triangle BMM_{1}} \, (*)[/tex]. Ето защо е необходимо предварително да намерим [tex]S_{\triangle BCC_{1}}, \, S_{\triangle COM}[/tex] и [tex]S_{\triangle BMM_{1}}[/tex].
За [tex]\triangle BMM_{1}[/tex] е лесно – [tex]S_{\triangle BMM_{1}}=\frac{1}{2}.BM.MM_{1}. sin \angle BMM_{1} \Leftrightarrow S_{\triangle BMM_{1}}=\frac{3a^2 cos\beta}{10} \, (1)[/tex].
За [tex]\triangle COM[/tex] – също – [tex]S_{\triangle COM}=\frac{1}{2}.CO.CM. sin \angle OCM \Leftrightarrow S_{\triangle COM}=\frac{1}{2}.\frac{7}{5}a.a. cos {\frac{\alpha+\beta}{2}} \Leftrightarrow S_{\triangle COM}=\frac{7a^2}{10} cos {\frac{\alpha+\beta}{2}} \, (2)[/tex].
От синусовата теорема за [tex]\triangle BCC_{1}[/tex] пресмятаме [tex]\frac{BC}{sin \angle BC_{1}C}=\frac{CC_{1}}{sin \angle CBC_{1}} \Leftrightarrow \frac{2a}{cos {\frac{\beta-\alpha}{2}}}=\frac{CC_{1}}{sin\beta} \Leftrightarrow CC_{1}=\frac{2a sin\beta}{cos {\frac{\beta-\alpha}{2}}}[/tex]. Сега от последното намираме и третото ни нужно лице – [tex]S_{\triangle BCC_{1}}=\frac{1}{2}.CC_{1}.BC. sin \angle BCC_{1} \Leftrightarrow S_{\triangle BCC_{1}}=\frac{1}{2}.\frac{2a sin \beta}{cos {\frac{\beta-\alpha}{2}}}.2a. cos {\frac{\alpha+\beta}{2}} \Leftrightarrow S_{\triangle BCC_{1}}=\frac{2a^2 sin \beta}{cos {\frac{\beta-\alpha}{2}}} cos {\frac{\alpha+\beta}{2}} \, (3)[/tex].
Вече от [tex](*)[/tex] определяме [tex]S_{OC_{1}M_{1}M}=(3)-(2)-(1) \Leftrightarrow S_{OC_{1}M_{1}M}=\frac{a^2}{10} (10 sin \beta cos {\frac{\alpha+\beta}{2}} - 3 cos {\frac{\beta-\alpha}{2}} - 7 cos {\frac{\alpha+\beta}{2}} cos {\frac{\beta-\alpha}{2}})[/tex].
| Description: |
|
| Големина на файла: |
20.29 KB |
| Видяна: |
2149 пъти(s) |
|
|
|
| Върнете се в началото |
|
 |
stefan_vn
Начинаещ
Регистриран на: 07 Dec 2009
Мнения: 3
 
|
 Пуснато на: Wed Dec 09, 2009 9:32 am Заглавие: Пуснато на: Wed Dec 09, 2009 9:32 am Заглавие: |
|
|
| Да мерси много . Задачата беше лесна
|
|
| Върнете се в началото |
|
 |
|
|
Не Можете да пускате нови теми
Не Можете да отговаряте на темите
Не Можете да променяте съобщенията си
Не Можете да изтривате съобщенията си
Не Можете да гласувате в анкети
Може да прикачвате файлове
Може да сваляте файлове от този форум
|
|