 Регистрирайте се Регистрирайте се
някой да реши няколко задачки :)
|
| Предишната тема :: Следващата тема |
| Автор |
Съобщение |
jessicca_077
Начинаещ
Регистриран на: 05 Nov 2009
Мнения: 11
 
|
 Пуснато на: Thu Nov 05, 2009 9:48 pm Заглавие: някой да реши няколко задачки :) Пуснато на: Thu Nov 05, 2009 9:48 pm Заглавие: някой да реши няколко задачки :) |
|
|
Моля,който може да я реши  Благодаря предв! Благодаря предв!
| Description: |
| да се реши чрез графичния метод оптимизационната зад!отг:Zmax=7,8;X1=12/5,X2=3/5 |
|
| Големина на файла: |
296.58 KB |
| Видяна: |
1627 пъти(s) |
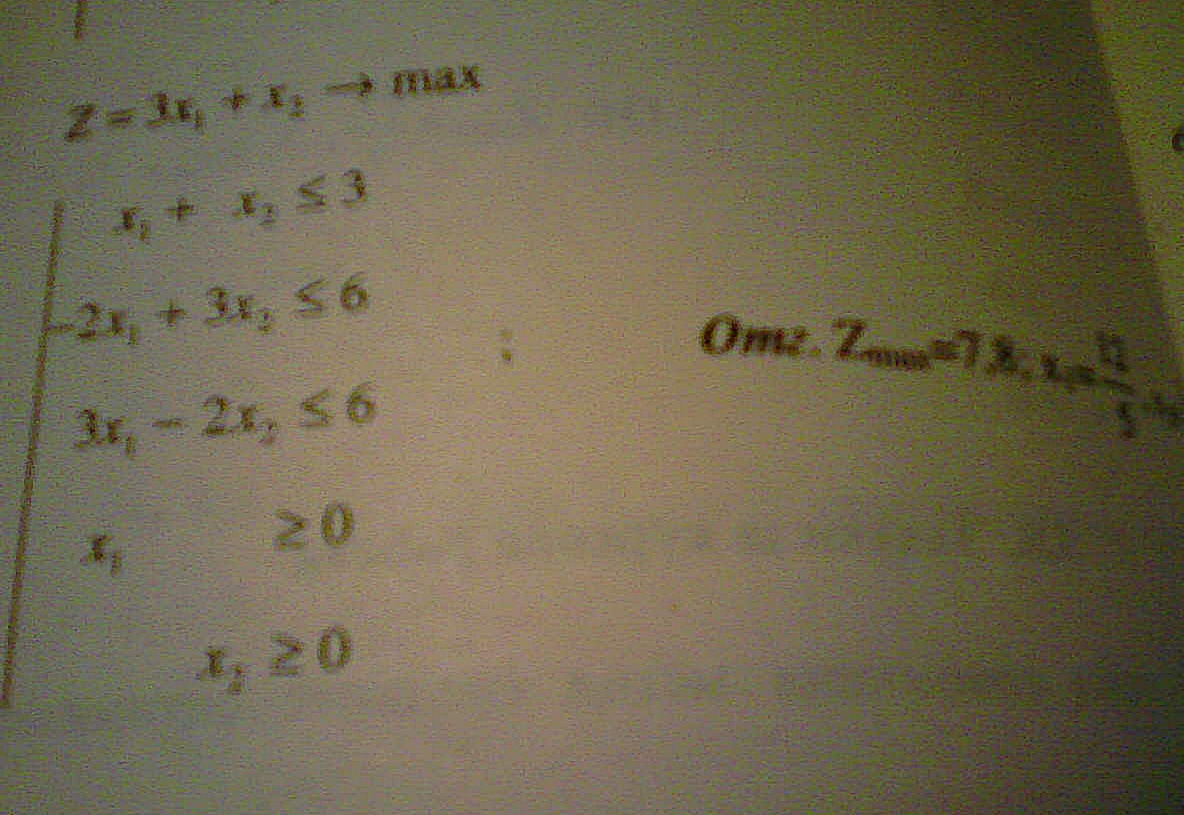
|
| Description: |
| права линия в равнина ...на втория ред в началото е основата АВ.. |
|
| Големина на файла: |
204.5 KB |
| Видяна: |
1627 пъти(s) |

|
|
|
| Върнете се в началото |
|
 |
Реклама
|
 Пуснато на: Заглавие: Реклама Пуснато на: Заглавие: Реклама |
|
|
|
|
|
| Върнете се в началото |
|
 |
stflyfisher
Напреднал
Регистриран на: 26 Jan 2009
Мнения: 394
    
гласове: 10
|
 Пуснато на: Fri Nov 06, 2009 7:54 am Заглавие: Пуснато на: Fri Nov 06, 2009 7:54 am Заглавие: |
|
|
Снимките за много лоши. По-добре напиши условията 
|
|
| Върнете се в началото |
|
 |
Добромир Глухаров
Редовен

Регистриран на: 19 Sep 2008
Мнения: 148
Местожителство: София
   
гласове: 8
|
 Пуснато на: Fri Nov 06, 2009 10:56 am Заглавие: Пуснато на: Fri Nov 06, 2009 10:56 am Заглавие: |
|
|
На първата задача отговорът
[tex]Z_{max}=Z_{x_1=\frac{12}{5 } ,x_2=\frac{3}{5 }}=\frac{39}{5 }[/tex] ли е?
|
|
| Върнете се в началото |
|
 |
jessicca_077
Начинаещ
Регистриран на: 05 Nov 2009
Мнения: 11
 
|
 Пуснато на: Fri Nov 06, 2009 11:03 am Заглавие: :) Пуснато на: Fri Nov 06, 2009 11:03 am Заглавие: :) |
|
|
май е по добре
...
а др зад е:
За равнобедрен трапец АВСD са дад. уравненията на основата АВ: x+y-15=0,бедрото AD:3x-y+27=0 и върхът С(-3,-2).Да се намерят останалите върхове.
отг.А(-3,1 , В(12,3),D(-8,3) , В(12,3),D(-8,3)
| Description: |
|
| Големина на файла: |
66.83 KB |
| Видяна: |
1581 пъти(s) |
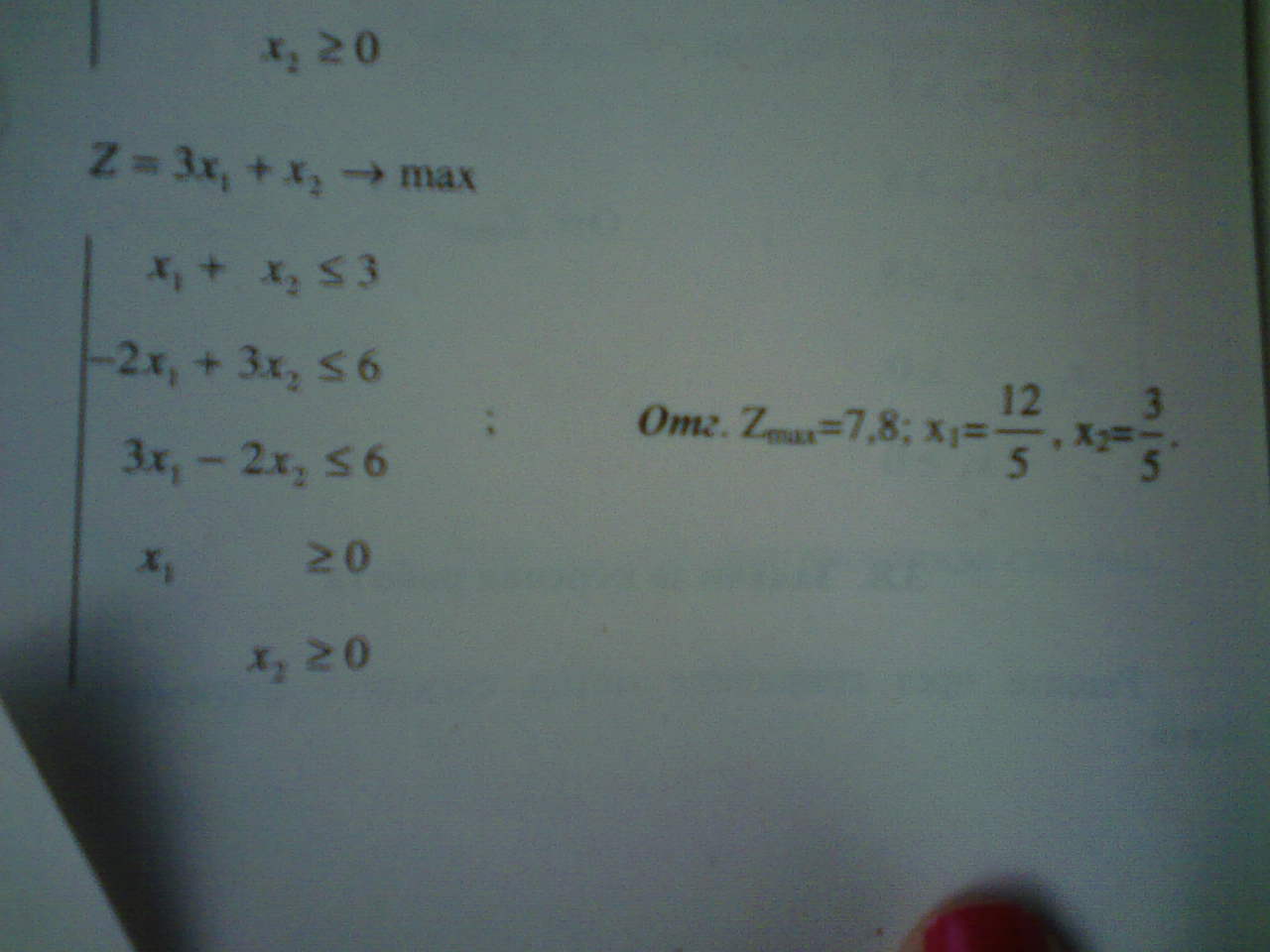
|
|
|
| Върнете се в началото |
|
 |
Добромир Глухаров
Редовен

Регистриран на: 19 Sep 2008
Мнения: 148
Местожителство: София
   
гласове: 8
|
|
| Върнете се в началото |
|
 |
stflyfisher
Напреднал
Регистриран на: 26 Jan 2009
Мнения: 394
    
гласове: 10
|
 Пуснато на: Fri Nov 06, 2009 11:59 am Заглавие: Пуснато на: Fri Nov 06, 2009 11:59 am Заглавие: |
|
|
[tex]AB\cap AD=A=>A:\begin {tabular}{|}x+y-15=0\\3x-y+27=0 \end{tabular}=>A(x_A,y_A)[/tex]
[tex]AB:x+y-15=0<=>y=-x+15=>k_{AB}=-1[/tex]
[tex] CD:y=k_{CD}x+n[/tex]
ABCD-трапец, АВ, CD-основи=>
[tex]AB\parallel CD=>k_{AB}=k_{CD}=-1=>CD:y=-1x+n[/tex] (  ) )
[tex] C(-3;-2) \in CD=>-2=-1(-3)+n=>n=5=>CD:y=-x-5[/tex]
[tex]CD\cap AD=D=>D:\begin {tabular}{|}3x-y+27=0 \\y=-x-5\end{tabular} =>D(x_D,y_D)[/tex]
ABCD- равнобедрен трапец, АВ, AD-бедра=>
[tex]|AD|=|CB|=>|AD|^2=|CB|^2=>\vec{AD}^2=\vec{CD}^2[/tex]
[tex]\vec{AD}(x_D-x_A,y_D-y_A)=>\vec{AD}^2=(x_D-x_A)^2+(y_D-y_A)^2[/tex]
[tex]\vec{CB}(x_B-x_C,y_B-y_C)=>\vec{CB}^2=(x_B-x_C)^2+(y_B-y_C)^2=>[/tex]
[tex](x_D-x_A)^2+(y_D-y_A)^2=(x_B-x_C)^2+(y_B-y_C)^2[/tex]
[tex]B(x_B,y_B) \in AB=>y_B=-x_B-15[/tex]
[tex]\begin {tabular}{|}y_B=-x_B-15\\(x_D-x_A)^2+(y_D-y_A)^2=(x_B-x_C)^2+(y_B-y_C)^2\end{tabular} =>B(x_B,y_B)[/tex]
|
|
| Върнете се в началото |
|
 |
jessicca_077
Начинаещ
Регистриран на: 05 Nov 2009
Мнения: 11
 
|
 Пуснато на: Fri Nov 06, 2009 12:25 pm Заглавие: до stflyfisher Пуснато на: Fri Nov 06, 2009 12:25 pm Заглавие: до stflyfisher |
|
|
благодаря за решението,нз дали не ставам нахална,но някакъв чертеж,защото аз въобще не я разбирам 
|
|
| Върнете се в началото |
|
 |
|
|
Не Можете да пускате нови теми
Не Можете да отговаряте на темите
Не Можете да променяте съобщенията си
Не Можете да изтривате съобщенията си
Не Можете да гласувате в анкети
Може да прикачвате файлове
Може да сваляте файлове от този форум
|
|