Окръжност, точка и хорда

[Spider Iovkov]

В окръжност с радиус [tex]R[/tex] е дадена хорда [tex]AB[/tex]. Нека [tex]M[/tex] е произволна точка от окръжността. Върху лъча [tex]MA[/tex] е нанесена отсечка [tex]MN[/tex], [tex]MN=R[/tex], а върху лъча [tex]MB[/tex] − отсечка [tex]MK[/tex], равна на разстоянието от [tex]M[/tex] до ортоцентъра на [tex]\triangle MAB[/tex]. Да се намери [tex]NK[/tex], ако по-малката от дъгите [tex]AB[/tex] има мярка [tex]2\alpha[/tex].

Упътване. Разгледайте два варианта за положението на точка [tex]M[/tex] върху окръжността.

[Реклама]

[ганка симеонова]

Емо, пусни от онзи сборник нещо готино
Дето има повече мслене.. Иначе

[tex]1) NK=R [/tex], ако M е в/у по-голямата дъга или
[tex]2)NK=R\sqrt{1+8cos^2\alpha } [/tex], ако е в/у по- малката.

[Spider Iovkov]

Окръжността, вписана в [tex]\triangle ABC[/tex], се допира до [tex]AC[/tex] в точка [tex]M[/tex], а до страната [tex]BC[/tex] − в точка [tex]N[/tex]. Ъглополовящата [tex]l_{a}[/tex] пресича правата [tex]MN[/tex] в точка [tex]K[/tex], а [tex]l_{b}[/tex] пресича същата права в точка [tex]L[/tex]. Да се докаже, че от отсечките [tex]MK, \, NL, \, KL[/tex] може да се построи триъгълник. Да се намери лицето на този триъгълник, ако [tex]S_{\triangle ABC}=S[/tex] и [tex]\angle ACB=\gamma[/tex].

[ганка симеонова]

На това вече му се казва КРАСИВА ЗАДАЧА

Очевидно следните триъгълници са подобни (защо?)
[tex]\Delta LIK; \Delta AIB;\Delta ALK [/tex]
Построяваме и третата допирна точка на вп окр с АВ-т.Т. Очевидно BS е симетрала за TN, но [tex]L\in BS=>\Delta TLN[/tex]-равнобедрен. Аналогично [tex]\Delta MTK [/tex]-равнобедрен. Тогава [tex]LT=LN; KM=KT [/tex].
И тъй като LT, TK, LK образуват триъгълник, то и LK,LN,MK образуват триъгълник и това е [tex]LTK[/tex]
[tex]\angle LNI=\angle CNI-\angle CNL=90^\circ -(90^\circ -\frac{\gamma }{2 } )=\frac{\gamma }{2 }[/tex]
Аналогично [tex]\angle KTI=\frac{\gamma }{2 }=>\angle LTK=\gamma =>[/tex]триъгълниците [tex]\Delta LTK; \Delta ABC [/tex] са подобни с коефициент [tex]\frac{LK}{ AB} [/tex]
Да разгледаме [tex]ATIL:\angle IAT=\angle ILT=>ATIL- [/tex]вписан=>[tex]\angle ALI=90^\circ [/tex]
Казахме, че [tex]\Delta LIK; \Delta AIB [/tex]са подобни=>[tex]k=\frac{LK}{AB}=\frac{LI}{IA } =cos\angle LIA=cos(180^\circ -\angle AIB)=cos(90^\circ -\frac{\gamma }{2 })=sin{\frac{\gamma }{2 }}[/tex]
=>[tex]S_{LTK}=k^2S=S.sin^2{\frac{\gamma }{2 }} [/tex]

ПП 5280 ми мнение

[Spider Iovkov]

Ганке... no words, ... Твоето решение е... просто най-най-най-доброто! Честно, уникално е! Уникално, , , , ! Направо... не мога да кажа нищо повече, , ...

[ганка симеонова]

Не знам, дали е най- доброто , може да има и по- добро, но лично аз си го харесвам. Мисля, че е доста изчистено.
ЗА сметка на това, днес вместо да си направя тематичните планове за 11 и 12 клас, решавах задачата
Ако и утре направя така, в понеделник няма да ме похвалят.

[martosss]

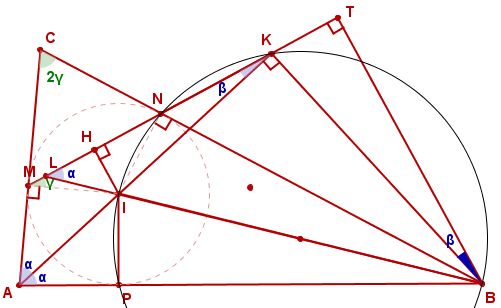
[tex]\angle MIN=180^\circ - 2\gamma,\;\;MI=IN=r\Right \angle IMN=\gamma[/tex]
[tex]\angle AKM=180^\circ -\alp -90^\circ -\gamma=\be[/tex]
Аналогично [tex]\angle BLK=\alp\Right\Del ABI\approx\Del LIK\Right {LK\over AB}={h_{LK}\over h_{AB}}={IH\over IP}={IH\over IM}=sin\gamma\Right\;\;\;[/tex][tex]\red\fbox{\frac{LK}{AB}=\sin\gamma}\left(1\right)[/tex]
От друга страна [tex]\angle MNC=90-\gamma =\alp +\be=\angle BAI+\angle ABI=\angle BIK\Right[/tex] около [tex]IBKN[/tex] може да се опише окръжност [tex]\Right \angle IKB=\angle INB=90^\circ[/tex], тоест [tex]BN[/tex] е височина в [tex]\Del ABI[/tex].
Нека също така спуснем височина [tex]BT[/tex] от [tex]B[/tex] в [tex]\Del LKB[/tex].

Сега [tex]\angle BKT=90^\circ -\be\Right \angle KBT=\be[/tex]
Тогава [tex]\Del BNL\approx\Del BIA\Right \frac{NL}{AI}=\frac{h_{NL}}{h_{AI}}=\frac{BT}{BK}=\cos \be\Right\;\;\;\fbox{NL=AI\cos \be}[/tex].
Сега от [tex]\Del AIC\Right^{Sin\; T.} \frac{AC}{\sin(90+\be)}=\frac{AI}{\sin\gamma}\Right \fbox{AI\cos\be =AC\sin\gamma}[/tex]
От горните две заключения получаваме, че [tex]NL=AC\sin\gamma\Right\;\;\;[/tex][tex]\red \frac{NL}{AC}=sin\gamma\;\;\; (2)[/tex]
Аналогично на (2) получаваме, че [tex]\frac{KM}{BC}=sin\gamma\;\;\; (3)[/tex]
От (1), (2) и (3) => [tex]\frac{MK}{AB}=\frac{NL}{AC}=\frac{KM}{BC}=sin\gamma[/tex]. Това означава, че отсечките [tex]LK, NL[/tex] и [tex]MK[/tex] са страни на триъгълник, който е подобен на триъгълник АВС с коефициент на подобие [tex]k=sin\gamma[/tex], където [tex]\gamma=\frac{\angle ACB}{2}[/tex]. това означава, че за лицето [tex]S_1[/tex] на този триъгълник имаме:
[tex]S_1=Sk^2=S\sin^2\gamma_1[/tex], където [tex]\gamma_1=\angle ACB[/tex]

[Grievery]

Наистина... решенията Ви са невероятни! Само един въпрос... как ги правите тези уникални чертежи?

[ганка симеонова]

Изтегли си CarMetal - програма за чертежи

http://carmetal.uptodown.com/en/

За целта трябва да имаш инсталирана JAVA

[r2d2]

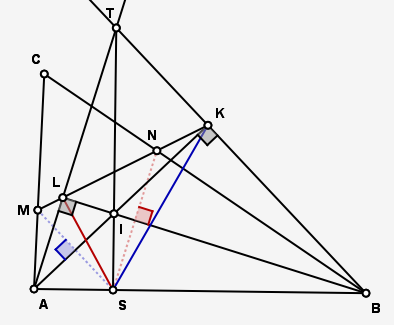
Лесно се доказва (тази задача е решавана във форума), че [tex]\angle AKB=\angle ALB = 90^circ.[/tex] Продължаваме AL и BK до пресичането им в Т. I e ортоцентърът на [tex]\Delta ABT[/tex], а [tex]\Delta LKS[/tex] е педалния му триъгълник.

Ъглите на [tex]\Delta ABT[/tex] са [tex]\angle A = 90 - \beta/2 \; \angle B=90 - \alpha/2 \; \angle T = 90 - \gamma /2 [/tex].
Лесно се пресмятат и ъглите на педалния: [tex]\angle S = 180 - 2\angle T= \gamma \; \angle K=180 - 2\angle A= \beta \Rightarrow \Delta SKL \sim \Delta CBA[/tex] с коефициент на подобие[tex] k=\frac {KL}{BA}.[/tex] Знаем, че [tex]\Delta CLK \sim \Delta CBA (k=\cos \angle T=\cos (90 - \gamma/2)=\sin \gamma/2).[/tex] T.e. [tex]\frac {KL}{BA}=\sin \gamma/2.[/tex]

При симетрия отн. АК М се изобразява в S т.е. [tex]MK = SK[/tex] и аналогично при сим. относно BL N->S т.е. [tex]LN=LS[/tex].