Обем на неправилно тяло

[Spider Iovkov]

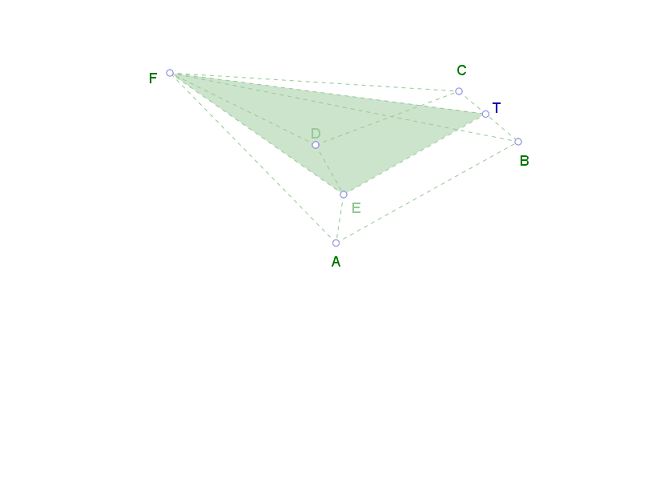
Нека е даден многостенът от картинката и той да е такъв, че [tex]FE\bot ABCDE, \, AB \cancel {||} CD, \, \angle AED=120^\circ[/tex]. Също така ъгълът между равнините [tex]ABCDE[/tex] и [tex]BCF[/tex] има мярка [tex]\varphi[/tex] и [tex]AB=CD=m, \, ET=n, \, AE=\frac{a}{2}, \, DE=a, \, BT=\frac{b}{3}, \, CT=b[/tex]. Да се намери обемът на многостена [tex]ABCDEF[/tex], ако:
а) [tex]a[/tex] и [tex]b[/tex] са числено равни съответно на [tex]2x[/tex] и [tex]cos y[/tex], където [tex]x[/tex] и [tex]y[/tex] удовлетворяват системата [tex]\begin{array}{||} x^2+2x sin y +1=0 \\ 8|x|y(x^2+y^2)+\pi^3+4\pi=0 \end{array}[/tex];
б) [tex]m[/tex] е коренът на уравнението [tex][\log_{4}(2x+9)+1]\log_{x+2}2=1[/tex];
в) [tex]n[/tex] е равно на утроената стойност на най-голямото цяло число [tex]b[/tex], за което функцията [tex]f(x)=\frac{bx+4}{b+x}[/tex] е намаляваща в цялата си дефиниционна област;
г) [tex]sin\varphi[/tex] е равен на корена на уравнението [tex]\log_{1-2x^2}=\frac{1}{4}-\frac{3}{4\log_{2}(1-2x^2)}[/tex];
д) около четириъгълниците [tex]ABTE[/tex] и [tex]ETCD[/tex] могат да се опишат окръжности;
е) диагоналът [tex]BE[/tex] е равен на сумата от двете крайни числа, заграждащи десния интервал на решения на неравенството [tex]\log_{\frac{25-x^2}{16}}(\frac{24-2x-x^2}{14})>1[/tex] − т. е. ако решението е от вида [tex](a;b) \cup (c;d)[/tex], то диагоналът е [tex]d_{0}=c+d[/tex];
ж) диагоналът [tex]DT[/tex] е равен на [tex]\tan{\frac{\alpha}{2}}[/tex] от уравнението [tex]135 sin\alpha + 54.\frac{8 \tan{\frac{\alpha}{2}}}{16 \tan^2{\frac{\alpha}{2}}+1}=27.8 \tan{\frac{\alpha}{2}}[/tex].

[Реклама]

[ганка симеонова]

Сега, Емо дори и да ми се обидиш, ще си напиша мнението за задачата.
Самото условие ме отблъсква. Това са задачи от едновремешен тип, при които " с един куршум се стрелят много зайци"...
Красотата на стереометрията, не е в упражняване на решаване на купища лог. и триг. уравнения и пр., а в нещо друго.
Аз не бих имала търпението, да сметна всички тези параметри, които са необходими.

П.П. Искаш ли да видиш красива стереометрична задача?

[Spider Iovkov]

Хайде, . А пък който е хитър, може да реши задачата само с буквичките, без да търси точните стойности на величините, по този начин се решава един общ случай, .

[ганка симеонова]