| Предишната тема :: Следващата тема |
| Автор |
Съобщение |
Vladi_mnt
Редовен
Регистриран на: 17 Apr 2009
Мнения: 113
         
гласове: 5
|
 Пуснато на: Fri Aug 14, 2009 3:31 pm Заглавие: задачата за Кьонингберските острови Пуснато на: Fri Aug 14, 2009 3:31 pm Заглавие: задачата за Кьонингберските острови |
|
|
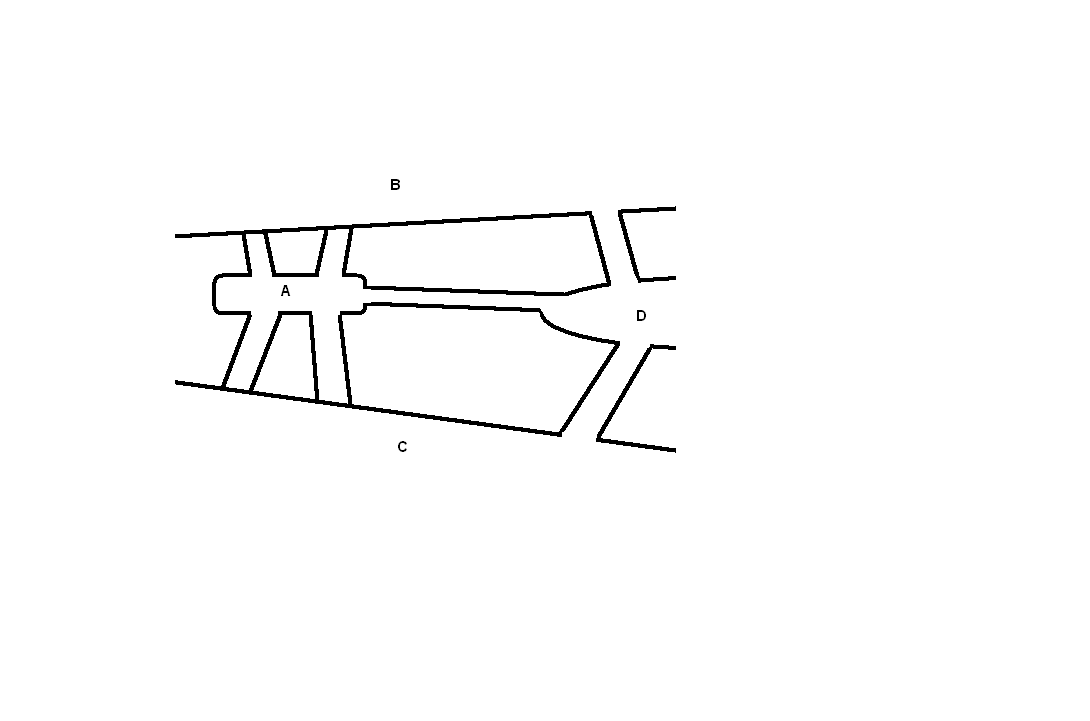
През 1736г. швейцарският математик Леонард Ойлер публикува първата работа от теория на графите - решението на задачата за Кьoнингберските мостове (Къонинберг = Калининград) има 7 мостове, които свързват два острова и бреговете на две сливащи се реки, както е показано на чертежа:
| Description: |
|
| Големина на файла: |
17.69 KB |
| Видяна: |
2085 пъти(s) |
|
|
|
| Върнете се в началото |
|
 |
Реклама
|
 Пуснато на: Заглавие: Реклама Пуснато на: Заглавие: Реклама |
|
|
|
|
|
| Върнете се в началото |
|
 |
Vladi_mnt
Редовен
Регистриран на: 17 Apr 2009
Мнения: 113
         
гласове: 5
|
 Пуснато на: Fri Aug 14, 2009 3:33 pm Заглавие: Пуснато на: Fri Aug 14, 2009 3:33 pm Заглавие: |
|
|
| Широко разпространена била следната задача: Може ли човек да излезе от дома си, да направи разходка, като мине по всеки мост точно веднъж и да се върне обратно у дома? Приемаме, че домът му се намира на някое от местата A,B,C или D.
|
|
| Върнете се в началото |
|
 |
ганка симеонова
SUPER VIP

Регистриран на: 10 Jan 2008
Мнения: 5985
Местожителство: софия
    
гласове: 298
|
 Пуснато на: Fri Aug 14, 2009 3:46 pm Заглавие: Пуснато на: Fri Aug 14, 2009 3:46 pm Заглавие: |
|
|
Не е възможно, защото за да се извърши успешна разходка ( всеки мост да се мине само веднъж) всяка точка трябва да е свързана с четен брой линии.
В случая Калининград има 4 участъка суша, и от всеки излизат по нечетен брой мостове. Три точки имат по 3 моста, а една точка 5 моста.
|
|
| Върнете се в началото |
|
 |
ганка симеонова
SUPER VIP

Регистриран на: 10 Jan 2008
Мнения: 5985
Местожителство: софия
    
гласове: 298
|
 Пуснато на: Fri Aug 14, 2009 3:51 pm Заглавие: Пуснато на: Fri Aug 14, 2009 3:51 pm Заглавие: |
|
|
Задачата за тези мостове е т. нар. задача за мрежите в приложната математика, но тя подтикнала Ойлер да разгледа по- абстрактни мрежи.
Той открил една формула за всички мрежи.
[tex]V+R-L=1 [/tex]
V- броя на върховете ( пресичанията) в мрежата,
L-броя на линиите в мрежата,
R-броя на областите ( затворените части) в мрежата.
|
|
| Върнете се в началото |
|
 |
Vladi_mnt
Редовен
Регистриран на: 17 Apr 2009
Мнения: 113
         
гласове: 5
|
 Пуснато на: Fri Aug 14, 2009 4:06 pm Заглавие: Пуснато на: Fri Aug 14, 2009 4:06 pm Заглавие: |
|
|
| Веднага откликвам: Защо точно четен? Искам доказателство на НДУ един граф да е Ойлеров? (т.е. вътре в него да има Ойлеров цикъл, а НДУ е за всеки негов връх да е от четна степен)
|
|
| Върнете се в началото |
|
 |
ганка симеонова
SUPER VIP

Регистриран на: 10 Jan 2008
Мнения: 5985
Местожителство: софия
    
гласове: 298
|
 Пуснато на: Fri Aug 14, 2009 4:36 pm Заглавие: Пуснато на: Fri Aug 14, 2009 4:36 pm Заглавие: |
|
|
По средата на разходката, когато човек премине по някой участък, той трябва да влезе през един мост и да напусне през друг.
Има две изключения- когато човек започва или завършва разходката.
В началото той напуска участък от сушата и се нуждае от единствен мост за изход, а в края- само от един мост, за да влезе в него.
Ако разходката започва и приключва в различни участъци, за тези два участъка се допуска да имат нечетен брой мостове.
Ако разходката започва и завършва от една и съща точка, тя заедно с другите трябва да има четен брой мостове.
|
|
| Върнете се в началото |
|
 |
Vladi_mnt
Редовен
Регистриран на: 17 Apr 2009
Мнения: 113
         
гласове: 5
|
 Пуснато на: Fri Aug 14, 2009 5:23 pm Заглавие: Пуснато на: Fri Aug 14, 2009 5:23 pm Заглавие: |
|
|
Аз предлагам перифразирано на Ганка решение;
Нека имаме граф G. Минаваме по всеки мост <=> минаваме през всяко ребро.
Като минем по едно ребро (разрешено е по 1 път през всяко МАКС!!!) стигаме връх на графа. Той може да е начален(или краен - те съвпадат) или да е някъде по "пътя" ни, и ще го нарека "среден".
1сл. Ако е начален/краен, то ние трябва да пристигнем в него и да тръгнем от него, но по условие по ребро минаваме 1 път макс => имаме поне 2 ребра. Но четността на пристиганията и тръгванията е еднаква => общият брой ребра, които излизат от върха е четен.
2сл. Аналогично "средният" връх ако се пристига по х начина (разбирайте различни ребра) до него, то от него трябва да се излиза също по х начина, т.е. общо 2*х ребра излизат от този връх, т.е. той е четен.
|
|
| Върнете се в началото |
|
 |
|