Determinant of a Matrix

By Catalin David

Definition

The determinant of a square matrix A is the integer obtained through a range of methods using the elements of the matrix.

Notation

Let $ A = \begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$

$det(A) = \left|A\right| = \begin{vmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{vmatrix}$

Properties of the Determinant

1. If a matrix has a row or a column with all elements equal to 0 then its determinant is 0.
   
   Example 12
   $\begin{vmatrix} 1 & 4 & 2\\ 0 & 0 & 0\\ 3 & 9 & 5 \end{vmatrix}= 0$ or $\begin{vmatrix} 1 & 4 & 0\\ 4 & 2 & 0\\ 3 & 9 & 0 \end{vmatrix}=0$
2. If a matrix has two equal rows or two equal columns then its determinant is 0.
   
   Example 13
   $\begin{vmatrix} 1 & 4 & 2\\ 1 & 4 & 2\\ 3 & 9 & 5 \end{vmatrix}= 0$ or $\begin{vmatrix} 1 & 4 & 1\\ 4 & 2 & 4\\ 3 & 9 & 3 \end{vmatrix}=0$
3. If a matrix has two proportional rows or two proportional columns then its determinant is 0.
   
   Example 14
   $\begin{vmatrix} 1 & 4 & 2\\ 2 & 8 & 4\\ 3 & 9 & 5 \end{vmatrix}= 0$ (the first two lines are proportional)
   or
   $\begin{vmatrix} 8 & 4 & 7\\ 4 & 2 & 3\\ 18 & 9 & 8 \end{vmatrix}=0$ (the first two columns are proportional)
4. If a line or a column is the sum or the difference of other lines, respectively columns then the determinant is 0.
   
   Example 15
   $\begin{vmatrix} 1 & 4 & 2\\ 7 & 2 & 3\\ 8 & 6 & 5 \end{vmatrix}= 0$     $R_{1} +R_{2} =R_{3}$ or
   
   $ \begin{vmatrix} 9 & 12 & 3\\ 1 & 8 & 7\\ 5 & 7 & 2 \end{vmatrix}=0$     $C_{1}+C_{3}=C_{2}$
5. In a determinant, we can individually factor integers out of lines and columns.
   
   Example 16
   In determinant
   $\begin{vmatrix} 3 & 9 & 12\\ 5 & 1 & 8 \\ 7 & 4 & 2 \end{vmatrix}$, we factor 3 out of row 1 $(R_{1})$ and we get:
   $3 \cdot \begin{vmatrix} 1 & 3 & 4\\ 5 & 1 & 8\\ 7 & 4 & 2 \end{vmatrix}$, then we factor 2 out of column 3 $(C_{3})$:
   $6\cdot \begin{vmatrix} 1 & 3 & 2\\ 5 & 1 & 4\\ 7 & 4 & 1 \end{vmatrix}$
6. In a determinant we can add or subtract rows or columns to other rows, respectively columns and the value of the determinant remains the same.
   
   Example 17
   $\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 & 13\\ 3 & 8 \end{vmatrix}$
   Example 18
   $\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 & 5\\ 11 & 8 \end{vmatrix}$
7. In a determinant we can add or subtract multiples of lines or columns.
   
   Example 19
   $\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 & 34\\ 3 & 8 \end{vmatrix}$
   
   Example 20
   $\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 & 5\\ 7 & 8 \end{vmatrix}$
8. The determinant of a matrix is equal to the determinant of its transpose.
9. The determinant of the product of two square matrices is equal to the product of the determinants of the given matrices.

Minor of a Matrix

The determinant obtained through the elimination of some rows and columns in a square matrix is called a minor of that matrix.

Example 21
$A=\begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$

One of the minors of the matrix A is $\begin{vmatrix} 1 & 4\\ 5 & 3 \end{vmatrix}$ (obtained through the elimination of row 3 and column 3 from the matrix A)

Another minor is $\begin{vmatrix} 1 & 2 \\ 6 & 1 \end{vmatrix}$ (obtained through the elimination of row 2 and column 2 from the matrix A)

Example 22
$B=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix} $

One of the minors of the matrix B is $ \begin{vmatrix} 1 & 7 & 9\\ 8 & 3 & 2\\ 8 & 1 & 4 \end{vmatrix}$ (obtained through the elimination of row 1 and column 1 from the matrix B)

Another minor is $\begin{vmatrix} 1 & 7 \\ 8 & 3 \end{vmatrix}$ (obtained through the elimination of rows 1 and 4 and columns 1 and 4 from the matrix B)

Let $A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{pmatrix}$

We can associate the minor $\Delta_{i,j}$ (obtained through the elimination of row i and column j) to any element $a_{i,j}$ of the matrix A.

Example 23
$ A = \begin{pmatrix} 4 & 7\\ 2 & 9 \end{pmatrix}$

We have to determine the minor associated to 2. Since this element is found on row 2, column 1, then 2 is $a_{2,1}$.

We have to eliminate row 2 and column 1 from the matrix A, resulting in

The minor of 2 is $\Delta_{2,1} = 7$.

Example 24
$B=\begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$

We have to determine the minor associated to 7. Since this element is found on row 2, column 3, then 7 is $a_{2,3}$.

We have to eliminate row 2 and column 3 from the matrix B, resulting in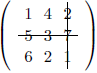

The minor of 7 is $\Delta_{2,3}= \begin{vmatrix} 1 & 4\\ 6 & 2 \end{vmatrix}$

Example 25
$C=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix}$

We have to determine the minor associated to 5. Since this element is found on row 1, column 2, then 5 is $a_{1,2}$.

We have to eliminate row 1 and column 2 from matrix C, resulting in

The minor of 5 is $\Delta_{1,2}= \begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$

The Cofactor of an Element of a Matrix

Let $A=\begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & a_{n,n}\\ \end{pmatrix}$

The cofactor $(-1)^{i+j}\cdot\Delta_{i,j}$ corresponds to any element $a_{i,j}$ in matrix A. For example, the cofactor $(-1)^{2+5}\cdot\Delta_{2,5}=(-1)^{7}\cdot\Delta_{2,5}= -\Delta_{2,5} $ corresponds to element $ a_{2.5}$

The Order of a Determinant

The order of a determinant is equal to its number of rows and columns.

Example 26
$\begin{vmatrix} 1 & 4\\ 6 & 2\\ \end{vmatrix}$ (it has 2 lines and 2 columns, so its order is 2)

Example 27
$\begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$ (it has 3 lines and 3 columns, so its order is 3)

Calculating the Determinant of a Matrix

The determinant of a matrix is equal to the sum of the products of the elements of any one row or column and their cofactors.

$\left| A\right| = \begin{vmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & a_{n,n}\\ \end{vmatrix}$

We can calculate the determinant using, for example, row i:

$\left| A\right| =a_{i,1}\cdot(-1)^{i+1}\cdot\Delta_{i,1}$ $+a_{i,2}\cdot(-1)^{i+2}\cdot\Delta_{i,2}+a_{i,3}\cdot(-1)^{i+3}\cdot\Delta_{i,3}+...$ $+a_{i,n}\cdot(-1)^{i+n}\cdot\Delta_{i,n}$

Alternatively, we can calculate the determinant using column j:

$\left| A\right| =a_{1,j}\cdot(-1)^{1+j}\cdot\Delta_{1,j}$ $+a_{2,j}\cdot(-1)^{2+j}\cdot\Delta_{2,j}+a_{3,j}\cdot(-1)^{3+j}\cdot\Delta_{3,j}+...$ $+a_{n,j}\cdot(-1)^{n+j}\cdot\Delta_{n,j}$

Calculating a 2x2 Determinant

We use row 1 to calculate the determinant.

$\left| A\right| = \begin{vmatrix} a_{1,1} & a_{1,2}\\ a_{2,1} & a_{2,2}\\ \end{vmatrix} = a_{1,1}\cdot(-1)^{1+1}\cdot\Delta_{1,1}+a_{1.2}\cdot(-1)^{1+2}\cdot\Delta_{1,2}=$

$a_{1,1}\cdot(-1)^{2}\cdot\Delta_{1,1}+a_{1.2}\cdot(-1)^{3}\cdot\Delta_{1,2}=a_{1,1}\cdot\Delta_{1,1}-a_{1.2}\cdot\Delta_{1,2}$

However, $ \Delta_{1,1}= a_{2,2} $ and $ \Delta_{1,2}=a_{2,1}$

$ \left| A\right| =a_{1.1} \cdot a_{2,2}- a_{1.2} \cdot a_{2,1}$

$\color{red}{ \begin{vmatrix} a & b\\ c & d \end{vmatrix} =a \cdot d - b \cdot c}$

Example 28
$\begin{vmatrix} 2 & 5\\ 3 & 8 \end{vmatrix} =2 \cdot 8 - 3 \cdot 5 = 16 -15 =1$

Example 29
$\begin{vmatrix} -4 & 7\\ -2 & 9 \end{vmatrix} =-4 \cdot 9 - 7 \cdot (-2) = -36 -(-14) =-36 + 14 = - 22$

Calculating a 3x3 Determinant

We use row 1 to calculate the determinant.

$ \left| A\right| = \begin{vmatrix} a_{1,1} & a_{1,2} & a_{1,3}\\ a_{2,1} & a_{2,2} & a_{2,3}\\ a_{3,1} & a_{3,2} & a_{3,3} \end{vmatrix} =$ $a_{1,1}\cdot(-1)^{1+1}\cdot\Delta_{1,1}+a_{1.2}\cdot(-1)^{1+2}\cdot\Delta_{1,2}$ $+a_{1.3}\cdot(-1)^{1+3}\cdot\Delta_{1,3}=$ $=a_{1,1}\cdot(-1)^{2}\cdot\Delta_{1,1}+a_{1.2}\cdot(-1)^{3}\cdot\Delta_{1,2}$ $+a_{1.3}\cdot(-1)^{4}\cdot\Delta_{1,3}=$ $a_{1,1}\cdot\Delta_{1,1}-a_{1.2}\cdot\Delta_{1,2}+a_{1.3}\cdot\Delta_{1,3}$

$\Delta_{1,1}= \begin{vmatrix} a_{2,2} & a_{2,3}\\ a_{3,2} & a_{3,3} \end{vmatrix} = a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2}$

$\Delta_{1,2}= \begin{vmatrix} a_{2,1} & a_{2,3}\\ a_{3,1} & a_{3,3} \end{vmatrix} = a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1}$

$\Delta_{1,3}= \begin{vmatrix} a_{2,1} & a_{2,2}\\ a_{3,1} & a_{3,2} \end{vmatrix} = a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1}$

$\left| A\right| =a_{1,1}\cdot( a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2})-a_{1,2}\cdot(a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1})+$ $a_{1,3}\cdot(a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1})=$ $a_{1,1}\cdot a_{2,2}\cdot a_{3,3}-a_{1,1}\cdot a_{2,3}\cdot a_{3,2}-a_{1,2}\cdot a_{2.1}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+$ $a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}=$ $\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-}$ $\color{red}{(a_{1,1}\cdot a_{2,3}\cdot a_{3,2}+a_{1,2}\cdot a_{2,1}\cdot a_{3,3}+a_{1,3}\cdot a_{2,2}\cdot a_{3,1})}$

To faster reach the last relation we can use the following method.

First, we rewrite the first two rows under the determinant, as follows.

We multiply the elements on each of the three red diagonals (the main diagonal and the ones underneath) and we add up the results:
$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}}$

We multiply the elements on each of the three blue diagonals (the secondary diagonal and the ones underneath) and we add up the results:

$\color{blue}{a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1}}$

If we subtract the two relations we get the determinant's formula:

$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-}$ $\color{red}{(a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1})}$

Example 30
$A=\begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{pmatrix}$

Example 31
$A=\begin{pmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{pmatrix}$

$= 3\cdot4\cdot9 + 1\cdot1\cdot1 + 7\cdot5\cdot2 -(1\cdot4\cdot7 + 2\cdot1\cdot3 + 9\cdot5\cdot1) =$ $ 108 + 1 + 70 -(28 + 6 + 45)=79-79=100$

There are determinants whose elements are letters. They can be calculated more easily using the properties of determinants. For example, we calculate the determinant of a matrix in which there are the same elements on any row or column, but reordered.

$\begin{vmatrix} a & b & c\\ c & a & b\\ b & c & a \end{vmatrix}$ $ \xlongequal{C_{1}+C_{2}+C_{3}} \begin{vmatrix} a + b + c & b & c\\ c + a + b & a & b\\ b + c + a & c & a \end{vmatrix} = (a + b + c) \cdot \begin{vmatrix} 1 & b & c\\ 1 & a & b\\ 1 & c & a \end{vmatrix}$

We calculate the last determinant:

$\begin{vmatrix} 1 & b & c\\ 1 & a & b\\ 1 & c & a \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 1 & b & c\\ 1 & a & b \end{array}$

$ = a^{2} + b^{2} + c^{2} -a\cdot c - b\cdot c - a\cdot b =$ $\frac{1}{2}\cdot(2a^{2} +2b^{2}+2c^{2} -2a\cdot b -2a\cdot c-2b\cdot c) =$ $\frac{1}{2}\cdot(a^{2}-2a\cdot b + b^{2}+ a^{2}-2a\cdot c +c^{2}+b^{2}-2b\cdot c + c^{2})=$ $\frac{1}{2}\cdot[(a-b)^{2}+(a-c)^{2}+(b-c)^{2}]$

In conclusion

$\begin{vmatrix} a & b & c\\ c & a & b\\ b & c & a \end{vmatrix}=$ $\frac{1}{2}\cdot(a+b+c)\cdot[(a-b)^{2}+(a-c)^{2}+(b-c)^{2}]$

Example 32
We calculate the determinant of a Vandermonde matrix.
$\begin{vmatrix} 1 & 1 & 1\\ a & b & c\\ a^{2} & b^{2} & c^{2} \end{vmatrix}$

Using the properties of determinants we modify row 1 in order to have two elements equal to 0. In this case, when we apply the formula, there's no need to calculate the cofactors of these elements because their product will be 0.

$\begin{vmatrix} 1 & 1 & 1\\ a & b & c\\ a^{2} & b^{2} & c^{2}\\ \end{vmatrix}$ $\xlongequal{C_{1}- C_{3}\\C_{2} -C_{3}} \begin{vmatrix} 0 & 0 & 1\\ a-c & b-c & c\\ a^{2}- c^{2} & b^{2}-c^{2} & c^{2} \end{vmatrix}=$ $1\cdot(-1)^{1+3}\cdot \begin{vmatrix} a-c & b-c \\ a^{2}- c^{2} & b^{2}-c^{2} \end{vmatrix}= $

$\begin{vmatrix} a-c & b-c \\ (a-c)(a+c) & (b-c)(b+c) \end{vmatrix}=$ $(a-c)(b-c)\begin{vmatrix} 1 & 1\\ a+c & b+c \end{vmatrix}=$

$=(a-c)(b-c)[(b+c)-(a+c)]=$ $(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)$

Calculating a 4x4 Determinant

In order to calculate 4x4 determinants, we use the general formula.

Before applying the formula using the properties of determinants:

1. We check if any of the conditions for the value of the determinant to be 0 is met.
2. We check if we can factor out of any row or column.
3. We check if the determinant is a Vandermonde matrix or if it has the same elements, but reordered, on any row or column.

In any of these cases, we use the corresponding methods for calculating 3x3 determinants. We modify a row or a column in order to fill it with 0, except for one element. The determinant will be equal to the product of that element and its cofactor. In this case, the cofactor is a 3x3 determinant which is calculated with its specific formula.

Example 33
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 0 & 0 & 0 & 0\\ 2 & 3 & 1 & 8 \end{vmatrix}$

We notice that all elements on row 3 are 0, so the determinant is 0.

Example 34
$\begin{vmatrix} 1 & 3 & 1 & 2\\ 5 & 8 & 5 & 3\\ 0 & 4 & 0 & 0\\ 2 & 3 & 2 & 8 \end{vmatrix}$
We notice that $C_{1}$ and $C_{3}$ are equal, so the determinant is 0.

Example 35
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 10 & 16 & 18 & 4\\ 2 & 3 & 1 & 8 \end{vmatrix}$
We notice that rows 2 and 3 are proportional, so the determinant is 0.

Example 36
$\begin{vmatrix} \color{red}{4} & 3 & 2 & 2\\ 0 & 1 & -3 & 3\\ 0 & -1 & 3 & 3\\ 0 & 3 & 1 & 1 \end{vmatrix}$

Since there is only one element different from 0 on column 1, we apply the general formula using this column. The cofactors corresponding to the elements which are 0 don't need to be calculated because the product of them and these elements will be 0.

=
$=4(1\cdot3\cdot1 +(-1)\cdot1\cdot3+3\cdot(-3)\cdot3$ $-(3\cdot3\cdot3+3\cdot1\cdot1 +1\cdot(-3)\cdot(-1)))$ $=4(3-3-27-(27+3+3))=4\cdot(-60)=-240$

Example 37
$\begin{vmatrix} 4 & 3 & 2 & 2\\ 0 & 1 & 0 & -2\\ 1 & -1 & 3 & 3\\ 2 & 3 & 1 & 1 \end{vmatrix}$

To modify rows to have more zeroes, we operate with columns and vice-versa. We pick a row or column containing the element 1 because we can obtain any number through multiplication.

We notice that there already two elements equal to 0 on row 2. We only make one other 0 in order to calculate only the cofactor of 1.

$\begin{vmatrix} 4 & 3 & 2 & 2\\ 0 & 1 & 0 & -2\\ 1 & -1 & 3 & 3\\ 2 & 3 & 1 & 1 \end{vmatrix} \xlongequal{C_{4}+2C_{2}}$ $\begin{vmatrix} 4 & 3 & 2 & 8\\ 0 & \color{red}{1} & 0 & 0\\ 1 & -1 & 3 & 1\\ 2 & 3 & 1 & 7 \end{vmatrix}=$ $=$

$= 1\cdot(-1)^{2+2}\cdot \begin{vmatrix} 4 & 2 & 8\\ 1 & 3 & 1\\ 2 & 1 & 7 \end{vmatrix}=$
$=4\cdot3\cdot7 + 1\cdot1\cdot8 + 2\cdot2\cdot1$ $-(8\cdot3\cdot2 + 1\cdot1\cdot4 + 7\cdot2\cdot1) =$ $ 84 + 8 + 4- 48-4-14=30$

Example 38
$\begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 3 & 3 & 3 & 3\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$

We can factor 3 out of row 3:
$3\cdot \begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 1 & 1 & 1 & 1\\ -1 & 4 & 2 & 1\\ \end{vmatrix}$

Since there are only elements equal to 1 on row 3, we can easily make zeroes.

$\begin{vmatrix} 1 & -2 & 3 & 2\\ 2 & 3 & 1 & -1\\ 1 & 1 & 1 & 1\\ -1 & 4 & 2 & 1 \end{vmatrix}$ $ \xlongequal{C_{1} - C_{4},C_{2}-C_{4},C_{3}-C_{4}} \begin{vmatrix} -1 & -4 & 1 & 2\\ 3 & 4 & 2 & -1\\ 0 & 0 & 0 & \color{red}{1}\\ -2 & 3 & 1 & 1 \end{vmatrix}$ $=1\cdot(-1)^{3+4}\cdot$ $=(-1)\cdot \begin{vmatrix} -1 & -4 & 1\\ 3 & 4 & 2 \\ -2 & 3 & 1\\ \end{vmatrix}$
$=-((-1)\cdot 4\cdot 1 +3 \cdot 3\cdot1 + (-2)\cdot (-4)\cdot 2$ $- (1\cdot 4\cdot (-2) + 2\cdot 3\cdot (-1) + 1\cdot (-4)\cdot3))$ $=-(-4 + 9 + 16 + 8 + 6 + 12) =-47$

Example 39
$\begin{vmatrix} 2 & 5 & 1 & 4\\ 4 & 1 & 6 & 3\\ 5 & 3 & 7 & 2\\ 1 & 0 & 2 & 4 \end{vmatrix}$

In this example, we can use the last row (which contains 1) and we can make zeroes on the first column.

$\begin{vmatrix} 2 & 5 & 1 & 4\\ 4 & 1 & 6 & 3\\ 5 & 3 & 7 & 2\\ 1 & 0 & 2 & 4 \end{vmatrix}$ $\xlongequal{R_{1}-2R_{4},R_{2}-4R_{4}, R_{3}-5R_{4}} \begin{vmatrix} 0 & 5 & -3 & -4\\ 0 & 1 & -2 & -13\\ 0 & 3 & -3 & -18\\ \color{red}{1} & 0 & 2 & 4 \end{vmatrix}=$ $=1\cdot(-1)^{4+1}\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & -3 & -4\\ 1 & -2 & -13\\ 3 & -3 & -18 \end{vmatrix}$

We factor -1 out of column 2 and -1 out of column 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 & 3 & 4\\ 1 & 2 & 13\\ 3 & 3 & 18 \end{vmatrix}=$ $-[5\cdot 2\cdot 18 + 1\cdot 3\cdot 4+ 3\cdot 3\cdot 13 - (4\cdot 2\cdot 3\cdot + 13\cdot 3\cdot 5 + 18\cdot 3\cdot 1)]=$ $-(180+12+117-24-195-54)=36$

Example 40
$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$

There is a 1 on column 3, so we will make zeroes on row 2.

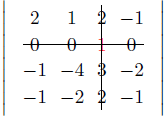$\begin{vmatrix} 4 & 7 & 2 & 3\\ 1 & 3 & 1 & 2\\ 2 & 5 & 3 & 4\\ 1 & 4 & 2 & 3 \end{vmatrix}$ $\xlongequal{C_{1}-C_{3}, C_{2}-3C_{3},C_{4}-2C_{3}} \begin{vmatrix} 2 & 1 & 2 & -1\\ 0 & 0 & \color{red}{1} & 0 \\ -1 & -4 & 3 & -2\\ -1 & -2 & 2 & -1 \end{vmatrix}=$ $=1\cdot(-1)^{2+5}\cdot \begin{vmatrix} 2 & 1 & -1\\ -1 & -4 & -2\\ -1 & -2 & -1 \end{vmatrix}$

We factor -1 out of row 2 and -1 out of row 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 2 & 1 & -1\\ 1 & 4 & 2\\ 1 & 2 & 1 \end{vmatrix}=$ $-[2\cdot 4\cdot 1 + 1\cdot 2\cdot (-1)+ 1\cdot 1\cdot 2 - ((-1)\cdot 4\cdot 1 + 2\cdot 2\cdot 2 + 1\cdot 1\cdot 1)]=$ $-(8-2+2+4-8-1)=-3$

Example 41
$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3\\ \end{vmatrix}$

We notice that any row or column has the same elements, but reordered. In this case, we add up all lines or all columns.

$\begin{vmatrix} 2 & 1 & 3 & 4\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{L_{1}+L_{2}+L_{3}+L_{4}} \begin{vmatrix} 10 & 10 & 10 & 10\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix} =$ $10\cdot \begin{vmatrix} 1 & 1 & 1 & 1\\ 1 & 3 & 4 & 2\\ 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 3 \end{vmatrix}$ $\xlongequal{C_{1} - C_{4},C_{2}-C_{4},C_{3}-C_{4}}10\cdot \begin{vmatrix} 0 & 0 & 0 & \color{red}{1}\\ -1 & 1 & 2 & 2\\ 2 & 3 & 1 & 1\\ 1 & -1 & -2 & 3 \end{vmatrix}=$

$=10\cdot1\cdot(-1)^{1+4}$

$ = (-10)\cdot \begin{vmatrix} -1 & 1 & 2\\ 2 & 3 & 1\\ 1 & -1 & -2 \end{vmatrix}=$ $(-10)\cdot((-1)\cdot 3\cdot (-2) +2 \cdot (-1)\cdot2 + 1\cdot 1\cdot 1$ $-(2\cdot 3\cdot 1 + 1\cdot (-1)\cdot (-1) + (-2)\cdot1\cdot2))$ $= -10\cdot(6 -4 +1 -6 - 1 + 4) =0$